题目内容
6. 如图所示,有一弯成θ=37°角的光滑金属导轨POQ,水平放置在磁感应强度为B=2T的匀强磁场中,磁场方向与导轨平面垂直.有一金属棒MN与导轨的OQ边垂直放置,金属棒从离O点右侧L0=10cm处静止开始以加速度a=0.2m/s2向右运动,求t=2秒末时,棒与导轨所构成的回路中的感应电动势多少?如果导体单位长度电阻为R0=2Ω,则导体中电流是多少?
如图所示,有一弯成θ=37°角的光滑金属导轨POQ,水平放置在磁感应强度为B=2T的匀强磁场中,磁场方向与导轨平面垂直.有一金属棒MN与导轨的OQ边垂直放置,金属棒从离O点右侧L0=10cm处静止开始以加速度a=0.2m/s2向右运动,求t=2秒末时,棒与导轨所构成的回路中的感应电动势多少?如果导体单位长度电阻为R0=2Ω,则导体中电流是多少?
分析 棒做匀加速运动,t=2s时,根据运动学位移公式和几何关系求出有效的切割长度L,由E=BLv求解回路中的感应电动势.求出回路的总电阻,再欧姆定律求感应电流.
解答 解:t=2s内棒的位移x=$\frac{1}{2}a{t}^{2}$=$\frac{1}{2}×0.2×{2}^{2}$m=0.4m,速度为 v=at=0.4m/s
回路有效的切割长度为 L=L0+xtanθ=0.1+0.4×tan37°=0.4m
回路中的感应电动势是 E=BLv=2×0.4×0.4V=0.32V
回路的总电阻 R=LR0=0.8Ω
电流 I=$\frac{E}{R}$=0.4A
答:棒与导轨所构成的回路中的感应电动势是0.32V,如果导体单位长度电阻为R0=2Ω,则导体中电流是0.4A.
点评 解决本题关键是确定导体棒有效的切割长度,即导体棒与导轨两个交点间的距离,掌握切割感应电动势公式和运动学公式,并能结合解题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
13.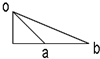 如图所示,一物体分别沿Oa、Ob轨道由静止滑下至底端,物体与轨道间的动摩擦因数相同.物体克服摩擦力做功分别是W1和W2则( )
如图所示,一物体分别沿Oa、Ob轨道由静止滑下至底端,物体与轨道间的动摩擦因数相同.物体克服摩擦力做功分别是W1和W2则( )
 如图所示,一物体分别沿Oa、Ob轨道由静止滑下至底端,物体与轨道间的动摩擦因数相同.物体克服摩擦力做功分别是W1和W2则( )
如图所示,一物体分别沿Oa、Ob轨道由静止滑下至底端,物体与轨道间的动摩擦因数相同.物体克服摩擦力做功分别是W1和W2则( )| A. | W1>W2 | B. | W1=W2 | C. | W1<W2 | D. | 无法比较 |
1.在“验证机械能守恒定律”实验中,在下面所列举的该实验的几个操作步骤中,你认为没有必要进行的或者错误的步骤是( )
| A. | 按照图示的装置安装器件 | |
| B. | 将打点计时器接到学生电源的直流输出端上 | |
| C. | 用天平测量出重物的质量 | |
| D. | 先放手让纸带和重物下落,再接通电源开关 | |
| E. | 在打出的纸带上,依据打点的先后顺序选取A、B、C、D(如图所示)四个合适的相邻点,通过测量计算得出B、C两点的速度为vB、vC,并测出B、C两点间的距离为h | |
| F. | 在误差允许范围内,看减少的重力势能mgh是否等于增加的动能$\frac{1}{2}$mv${\;}_{C}^{2}$-$\frac{1}{2}$mv${\;}_{B}^{2}$,从而验证机械能守恒定律 |
18. 如图所示,为早期制作的发电机及电动机的示意图,A盘和B盘分别是两个可绕固定转轴转动的铜盘,用导线将A盘的中心和B盘的边缘连接起来,用另一根导线将B盘的中心和A盘的边缘连接起来.当A盘在外力作用下转动起来时,B盘也会转动.则下列说法中正确的是( )
如图所示,为早期制作的发电机及电动机的示意图,A盘和B盘分别是两个可绕固定转轴转动的铜盘,用导线将A盘的中心和B盘的边缘连接起来,用另一根导线将B盘的中心和A盘的边缘连接起来.当A盘在外力作用下转动起来时,B盘也会转动.则下列说法中正确的是( )
 如图所示,为早期制作的发电机及电动机的示意图,A盘和B盘分别是两个可绕固定转轴转动的铜盘,用导线将A盘的中心和B盘的边缘连接起来,用另一根导线将B盘的中心和A盘的边缘连接起来.当A盘在外力作用下转动起来时,B盘也会转动.则下列说法中正确的是( )
如图所示,为早期制作的发电机及电动机的示意图,A盘和B盘分别是两个可绕固定转轴转动的铜盘,用导线将A盘的中心和B盘的边缘连接起来,用另一根导线将B盘的中心和A盘的边缘连接起来.当A盘在外力作用下转动起来时,B盘也会转动.则下列说法中正确的是( )| A. | 不断转动A盘就可以获得持续的电流,其原因是将整个铜盘看成沿径向排列的无数根铜条,它们做切割磁感线运动,产生感应电动势 | |
| B. | 当A盘转动时,B盘也能转动的原因是电流在磁场中受到力的作用,此力对转轴有力矩 | |
| C. | 当A盘顺时针转动时,B盘逆时针转动 | |
| D. | 当A盘顺时针转动时,B盘也顺时针转动 |
16.如图为“验证机械能守恒定律”的实验装置,下列哪些说法是正确的( )


| A. | 实验时应选用密度大体积小,并且下端有橡胶垫的重锤 | |
| B. | 实验时,当松开纸带让重锤下落同时,立即接通电源 | |
| C. | 要选用第1、2点间距离接近2mm的纸带 | |
| D. | 实验结果总是动能的增量略大于重力势能的减小量 |

 如图所示,ace和bdf是间距为L的两根足够长平行导轨,其中ac、bd段光滑,ce、df段粗糙,导轨平面与水平面的夹角为θ.整个装置处在磁感应强度为B,方向垂直于导轨平面向上的匀强磁场中,ab之间连有阻值为R的电阻.若将一质量为m的金属棒置于ef端,今用大小为F,方向沿斜面向上的恒力把金属棒从ef位置由静止推至距ef端s处的cd位置(此时金属棒已经做匀速运动),现撤去恒力F,金属棒最后又回到ef端(此时金属棒也已经做匀速运动).若不计导轨和金属棒的电阻,且金属棒与ce、df段的动摩擦因数为μ.
如图所示,ace和bdf是间距为L的两根足够长平行导轨,其中ac、bd段光滑,ce、df段粗糙,导轨平面与水平面的夹角为θ.整个装置处在磁感应强度为B,方向垂直于导轨平面向上的匀强磁场中,ab之间连有阻值为R的电阻.若将一质量为m的金属棒置于ef端,今用大小为F,方向沿斜面向上的恒力把金属棒从ef位置由静止推至距ef端s处的cd位置(此时金属棒已经做匀速运动),现撤去恒力F,金属棒最后又回到ef端(此时金属棒也已经做匀速运动).若不计导轨和金属棒的电阻,且金属棒与ce、df段的动摩擦因数为μ.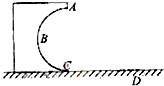 如图所示,一固定在竖直平面内的光滑的半圆形轨道ABC,其半径R=2.5m,轨道在C处与水平地面相切.在C处放质量为m=1kg的一小物块,给它一水平向左的初速度v0=10$\sqrt{2}$m/s,结果它沿CBA运动,并能通过A点,最后落在水平面上的D点,求:
如图所示,一固定在竖直平面内的光滑的半圆形轨道ABC,其半径R=2.5m,轨道在C处与水平地面相切.在C处放质量为m=1kg的一小物块,给它一水平向左的初速度v0=10$\sqrt{2}$m/s,结果它沿CBA运动,并能通过A点,最后落在水平面上的D点,求: