题目内容
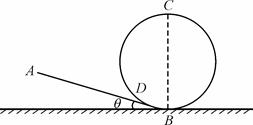
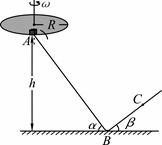
(12分)如图所示一水平圆盘绕过圆心的竖直轴转动,圆盘边缘有一质量m=1.0kg的小滑块。当圆盘转动的角速度达到某一数值时,滑块从圆盘边缘A点滑落,经光滑的过渡圆管进入轨道ABC。已知AB段斜面倾角为α=53°,BC段斜面倾角为β=37°,滑块与圆盘及斜面间的动摩擦因数均为μ=0.5,A点离B点所在水平面的高度h=1.2m。滑块在运动过程中始终未脱离轨道,不计在过渡圆管处和B点的机械能损失,最大静摩擦力近似等于滑动摩擦力,取g=10m/s2,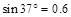 ,
,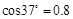 。求:
。求:
(1)若圆盘半径R=0.2m,滑块从圆盘上滑落时圆盘的角速度ω;
(2)取圆盘所在平面为零势能面,滑块到达B点时的机械能EB;
(3)滑块经过B点后0.6s内发生的位移xBC。
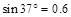 ,
,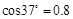 。求:
。求:
(1)若圆盘半径R=0.2m,滑块从圆盘上滑落时圆盘的角速度ω;
(2)取圆盘所在平面为零势能面,滑块到达B点时的机械能EB;
(3)滑块经过B点后0.6s内发生的位移xBC。
见解析
试题分析:(1)滑块在圆盘上做圆周运动时,受盘面静摩擦力作用,根据牛顿第二定律得:
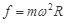 ①
①滑落时:
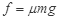 ②
②联解①②得:ω=5rad/s? ③
(2)滑块在离开A点滑落时的速度:
 ④
④滑块从A到B的运动过程,由动能定理得:
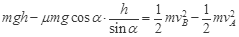 ⑤
⑤滑块在B点时的机械能:
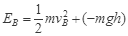 ⑥
⑥联解④⑤⑥得:
 ⑦
⑦(3)设滑块沿BC段向上做匀变速运动经过时间t1到达最高点后下滑,有:
上滑时:
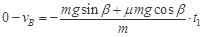 ⑧
⑧ ⑨
⑨下滑时:
 ⑩
⑩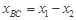 ?
?联解④⑤⑧⑨⑩?得:
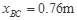 ?
?评分参考意见:本题满分12分,其中①~?式各1分;若有其他合理解法且答案正确,可同样给分。

练习册系列答案
相关题目

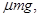 现用水平拉力F拉B,使A、B以同一加速度运动,则拉力F的最大值为
现用水平拉力F拉B,使A、B以同一加速度运动,则拉力F的最大值为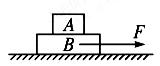
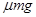 B.
B.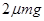 C.
C.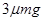 D.
D.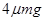
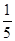 ,g取10 m/s2,求:
,g取10 m/s2,求: