题目内容
 在光滑的水平地面上方,有两个磁感应强度大小均为B,方向相反的水平匀强磁场,如图所示的PQ为两个磁场的边界,磁场范围足够大.一个半径为a、质量为m、电阻为R的金属圆环垂直磁场方向,以速度
在光滑的水平地面上方,有两个磁感应强度大小均为B,方向相反的水平匀强磁场,如图所示的PQ为两个磁场的边界,磁场范围足够大.一个半径为a、质量为m、电阻为R的金属圆环垂直磁场方向,以速度| 1 |
| 2 |
| 1 |
| 2 |
分析:由导体切割磁感线公式可求得感应电动势,由功率公式可求得电功率;由闭合电路欧姆定律可求得电路中的电流,则可求得安培力,由牛顿第二定律求得加速度;
由法拉第电磁感应定律可求得通过截面的电量;
由法拉第电磁感应定律可求得通过截面的电量;
解答:解:A、当直径与边界线重合时,圆环运动到直径刚好与边界线PQ重合时,圆环左右两半环均产生感应电动势,故线圈中的感应电动势E=2B×2a×
=2Bav;
圆环中的电功率P=
=
,故A正确;
B、此时圆环受力F=2BI×2a=2B?2
×2a=
,由牛顿第二定律可得,加速度a=
=
,故B错误;
C、电路中的平均电动势
=
,则电路中通过的电量Q=
△t=
△t=
=
,故C正确;
D、此过程中产生的电能等于电路中的热量,也等于外力所做的功,则一定也等于动能的改变量,故E=
mv2-
m(
)2=
mv2=0.375mv2.故D错误;
故选:AC.
| v |
| 2 |
圆环中的电功率P=
| E2 |
| R |
| 4B2a2v2 |
| R |
B、此时圆环受力F=2BI×2a=2B?2
| Bav |
| R |
| 8B2a2v |
| R |
| F |
| m |
| 8B2a2v |
| mR |
C、电路中的平均电动势
. |
| E |
| △Φ |
| △t |
. |
| I |
| ||
| R |
| △Φ |
| R |
| Bπa2 |
| R |
D、此过程中产生的电能等于电路中的热量,也等于外力所做的功,则一定也等于动能的改变量,故E=
| 1 |
| 2 |
| 1 |
| 2 |
| v |
| 2 |
| 3 |
| 8 |
故选:AC.
点评:本题考查电磁感应规律、闭合电路运算、感应电动势瞬时值与平均值应用等.关键为:搞清楚磁通量的变化、平动切割的有效长度、瞬时值与平均值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在光滑的水平地面上方,有两个磁感应强度大小均为B、方向相反的水平匀强磁场,如图所示PQ为两个磁场的边界,磁场范围足够大.一个半径为a,质量为m,电阻为R的金属圆环垂直磁场方向,以速度v从如图所示位置运动,当圆环运动到直径刚好与边界线PQ重合时,圆环的速度为v/2,则下列判断正确的是( )
在光滑的水平地面上方,有两个磁感应强度大小均为B、方向相反的水平匀强磁场,如图所示PQ为两个磁场的边界,磁场范围足够大.一个半径为a,质量为m,电阻为R的金属圆环垂直磁场方向,以速度v从如图所示位置运动,当圆环运动到直径刚好与边界线PQ重合时,圆环的速度为v/2,则下列判断正确的是( )
 在光滑的水平地面上方,有两个磁感应强度大小均为B、方向相反的水平匀强磁场,如图所示PQ为两个磁场的边界,磁场范围足够大.一个半径为a,质量为m,电阻为R的金属圆环垂直磁场方向,以速度v从如图所示位置运动,当圆环运动到直径刚好与边界线PQ重合时,圆环的速度为v/2,则此时圆环中的电功率
在光滑的水平地面上方,有两个磁感应强度大小均为B、方向相反的水平匀强磁场,如图所示PQ为两个磁场的边界,磁场范围足够大.一个半径为a,质量为m,电阻为R的金属圆环垂直磁场方向,以速度v从如图所示位置运动,当圆环运动到直径刚好与边界线PQ重合时,圆环的速度为v/2,则此时圆环中的电功率 在光滑的水平地面上方,有两个磁感应强度大小均为B、方向相反的水平匀强磁场,如图所示,PQ为两个磁场的边界,磁场范围足够大.一个半径为a,质量为m,电阻为R的金属圆环垂直磁场方向,以速度v从如图所示位置运动,当圆环运动到直径刚好与边界线PQ重合时,圆环的速度为
在光滑的水平地面上方,有两个磁感应强度大小均为B、方向相反的水平匀强磁场,如图所示,PQ为两个磁场的边界,磁场范围足够大.一个半径为a,质量为m,电阻为R的金属圆环垂直磁场方向,以速度v从如图所示位置运动,当圆环运动到直径刚好与边界线PQ重合时,圆环的速度为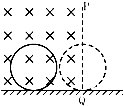 (2013?日照一模)在光滑的水平地面上方,有个磁感应强度大小B、方向垂直纸面向里的匀强磁场,如图PQ为磁场的边界.一个半径为a,质量为m,电阻为R的金属圆环垂直磁场方向,以速度v从如图位置运动,当圆环运动到直径刚好与边界线PQ重合时,圆环的速度为
(2013?日照一模)在光滑的水平地面上方,有个磁感应强度大小B、方向垂直纸面向里的匀强磁场,如图PQ为磁场的边界.一个半径为a,质量为m,电阻为R的金属圆环垂直磁场方向,以速度v从如图位置运动,当圆环运动到直径刚好与边界线PQ重合时,圆环的速度为