Question

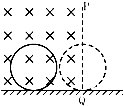（2013?日照一模）在光滑的水平地面上方，有个磁感应强度大小B、方向垂直纸面向里的匀强磁场，如图PQ为磁场的边界．一个半径为a，质量为m，电阻为R的金属圆环垂直磁场方向，以速度v从如图位置运动，当圆环运动到直径刚好与边界线PQ重合时，圆环的速度为

v

2

，则下列说法正确的是（　　）

• A．此时圆环中的电功率为

  4B2a2v2

  R

  ?
• B．此时圆环的加速度为

  2B2a2v

  mR

• C．此过程中通过圆环截面的电量为

  πBa2

  2R

• D．此过程中回路产生的电能为0.75mv²

Answer 1

分析：A、圆环的左半边切割磁感线，等效长度为2a，根据E=BLv，求出感应电动势，从而求出感应电流，根据P=I²R求出低昂率．
B、根据感应电流求出安培力，再根据牛顿第二定律求出加速度．
C、根据q=

.

I

t=

△Φ

R

，求出此过程中通过圆环截面的电量．
D、根据能量守恒求回路中产生的电能．

解答：解：A、当圆环运动到直径刚好与边界线PQ重合时，产生的感应电动势E=B×2a×

v

2

=Bav，感应电流I=

Bav

R

．所以P=I²R=

B2a2v2

R

．故A错误．
    B、金属圆环受到的安培力F=2BIa=

2B2a2v

R

．所以a=

F

m

=

2B2a2v

mR

．故B正确．
    C、q=

.

I

t=

△Φ

R

=

Bπa2

2R

．故C正确．
    D、有能量守恒得：产生的电能W_电=

1

2

mv2-

1

2

m(

v

2

)2=

3

8

mv2．故D错误．
故选BC．

点评：解决本题的关键掌握导体切割磁场产生的感应电动势E=BLv，知道L为有效长度．以及掌握电量q=

.

I

t=

N△Φ

R

．