题目内容
(8分)在竖直平面内有一个光滑的半圆轨道,轨道两端连线即直径在竖直方向,轨道半径为0.9m,一个质量为0.5kg的小球以一定的初速度滚上轨道(取g=10m/s2)。求:
(1)小球在最高点不脱离轨道的最小速率是多少?
(2)小球在最高点速率v=4m/s时,小球对轨道的压力是多少?
(1) (2)
(2) 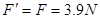
解析试题分析: (1)在最高点小球不脱离轨道的条件是重力不大于小球做圆周运动所需要的向心力
即 (1分)
(1分)
则所求的最小速率: (2分)
(2分)
(2)因为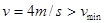 ,所以轨道对小球有一定的压力F
,所以轨道对小球有一定的压力F
则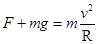 (2分)
(2分)
所以 (1分)
(1分)
由牛顿第三定律知,小球对轨道的作用力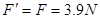 (2分)
(2分)
考点:本题考查绳、杆模型过最高点的条件。

练习册系列答案
相关题目
下图是摩托车比赛转弯时的情形.转弯处路面常是外高内低,摩托车转弯有一个最大安全速度,若超过此速度,摩托车将发生滑动.对于摩托车滑动的问题,下列论述正确的是( )
| A.摩托车一直受到沿半径方向向外的离心力作用 |
| B.摩托车所受外力的合力小于所需的向心力 |
| C.摩托车将沿其线速度的方向沿直线滑去 |
| D.摩托车将沿其半径方向沿直线滑去 |
一小船在静水中的速度为5 m/s,它在一条河宽为200 m,水流速度为3 m/s的河流中过河,则( )
| A.小船不可能垂直河岸抵达正对岸 |
| B.小船过河的时间不可能少于50 s |
| C.小船以最短航程过河时,过河的时间为40 s |
| D.小船以最短时间过河时,它沿水流方向的位移大小为120 m |
 、
、 为水平放置的间距
为水平放置的间距 的两块足够大的平行金属板,两板间有方向由
的两块足够大的平行金属板,两板间有方向由 。在
。在 ,油漆喷枪可向各个方向均匀地喷出初速度大小均为
,油漆喷枪可向各个方向均匀地喷出初速度大小均为 的油漆微粒,已知油漆微粒的质量均为
的油漆微粒,已知油漆微粒的质量均为 、电荷量均为
、电荷量均为 ,不计油漆微粒间的相互作用、油漆微粒带电对板间电场和磁场的影响及空气阻力,重力加速度
,不计油漆微粒间的相互作用、油漆微粒带电对板间电场和磁场的影响及空气阻力,重力加速度 。求:
。求:

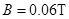 ,调节喷枪使油漆微粒只能在纸面内沿各个方向喷出,其它条件不变。
,调节喷枪使油漆微粒只能在纸面内沿各个方向喷出,其它条件不变。 。
。

 F
F F
F