题目内容
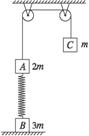
如图所示，质量为2m的物体A经一轻质弹簧与地面上的质量为3m的物体B相连，弹簧的劲度系数为k，一条不可伸长的轻绳绕过定滑轮，一端连物体A，另一端连一质量为m的物体C，物体A、B、C都处于静止状态.已知重力加速度为g,忽略一切摩擦.
（1）求物体B对地面的压力.
（2）把物体C的质量改为5m，并使C缓慢下降，最终A、B、C又处于静止状态，且C只受重力和绳的拉力作用，求此过程中物体A上升的高度.
（1）4mg (2)
解析:
（1）对于物体C，由平衡条件可得：
FT=mg ①
对于物体A、B及弹簧整体，由平衡条件可得：
FT+FN=5mg ②
由①②式得FN=4mg方向竖直向上 ③
根据牛顿第三定律可得FN′=FN=4mg,即物体B对地面的压力为4mg，方向竖直向下. ④
（2）对于物体A，初态时，由平衡条件得FT+kx1=2mg(x1为初态时弹簧压缩量) ⑤
对于物体C，末态时，由平衡条件得
FT′=5mg ⑥
对于物体A，末态时，由平衡条件得
FT′=2mg+kx2(x2为末态时弹簧拉伸量) ⑦
所求物体A上升的高度为h=x1+x2 ⑧
联立⑤⑥⑦⑧式解得h=
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图所示，质量为2m和m的可看做质点的小球A、B，用不计质量不可伸长的细线相连，跨在固定的光滑圆柱两侧，开始时，A球和B球与圆柱轴心同高，然后释放A球，则B球到达最高点时速率是多少？
如图所示，质量为2m的物块A和质量为m的物块B与地面的摩擦均不计，在已知水平恒力F的作用下，A、B一起做匀加速直线运动，则A对B的作用力大小为
如图所示，质量为2m的物块A和质量为m的物块B与地面的摩擦均不计．在已知水平推力F的作用下，A、B做加速运动．则由A和B组成的整体的加速度是
如图所示，质量为2m的物块A与水平地面的动摩擦因数为μ，质量为m的物块B与地面的摩擦不计，在大小为F的水平推力作用下，A、B一起向右做加速运动，则A和B之间的作用力大小为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示，质量为2m的木板，静止放在光滑的水平面上，木板左端固定着一根轻质弹簧，一质量为m的小木块（大小不计）从木板右端以末知速度v0开始沿木板向左滑行，最终回到木板右端刚好末从木板右端刚好末从木板滑，若在小木块压缩弹簧过程中，弹簧具有最大弹性势能为Ep，小木块与木板间滑动摩擦力的大小保持不变，求未知速度v0的大小．