��Ŀ����
12�� ��ͼ��ʾ�������ѹ��ԭ��Ȧa��b���˽����ҽ����ѹu=220$\sqrt{2}$sin100��t��V����ԭ������Ȧ��������n1��n2=10��1������������R�������ֵ��8������ֵ����R1=4����R2=8�������еĵ����Ϊ��������ڽ�������������ͷ�����϶�����R���м�Ĺ����У�����˵����ȷ���ǣ�������
��ͼ��ʾ�������ѹ��ԭ��Ȧa��b���˽����ҽ����ѹu=220$\sqrt{2}$sin100��t��V����ԭ������Ȧ��������n1��n2=10��1������������R�������ֵ��8������ֵ����R1=4����R2=8�������еĵ����Ϊ��������ڽ�������������ͷ�����϶�����R���м�Ĺ����У�����˵����ȷ���ǣ�������| A�� | ������A1ʾ�������ֵΪ0.2$\sqrt{2}$A | |
| B�� | ��ѹ��V2�͵�����A2ʾ���ij˻���������С | |
| C�� | ��ѹ��V1��ʾ���ȱ����С | |
| D�� | ��ֵ����R2���ĵĵ繦��һֱ��� |
���� ���ݱ�ѹ����Ȧ���˵�ѹ����Ȧ����������ѹ��V1��ʾ�����ڽ�������������ͷ�����϶�����R���м�Ĺ����У������������ϲ��ֺ�R1������Ȼ����²��ֲ�����
��Ч����ΪR�����ϲ��ֵ���Ϊx�����ݲ�����·�ص�ã�$R=\frac{��4+x����8-x��}{4+8}=\frac{��4+x����8-x��}{12}$$��\frac{��\frac{4+x+8-x}{2}��^{2}}{12}=3��$�����ҽ���4+x=8-x����x=2��ʱȡ�Ⱥţ��������Ż�����ͷ���ƹ��̣���Ч�����ȼ�С��������ŷķ�����жϵ����ı仯��
��� �⣺A���ڽ�������������ͷ�����϶�����R���м�Ĺ����У������������ϲ��ֺ�R1������Ȼ����²��ֲ�����
��Ч����ΪR�����ϲ��ֵ���Ϊx�����ݲ�����·�ص�ã�$R=\frac{��4+x����8-x��}{4+8}=\frac{��4+x����8-x��}{12}$$��\frac{��\frac{4+x+8-x}{2}��^{2}}{12}=3��$��
���ҽ���4+x=8-x����x=2��ʱȡ�Ⱥţ��������Ż�����ͷ���ƹ��̣���Ч�����ȼ�С�����������������������ѹ���䣬���Ե�ѹ��V1��ʾ�����䣬����ŷķ���ɿ�֪����Ȧ�ĵ�����������С��
��x=2��ʱ�������${I}_{2}=\frac{{U}_{2}}{{R}_{2}+R}=\frac{22}{4+3}A=\frac{22}{7}A$�����ݵ����������Ĺ�ϵ�ȿ�֪��������A1ʾ����������С��${I}_{1}=\frac{{n}_{2}}{{n}_{1}}{I}_{2}=\frac{1}{10}��\frac{22}{7}A=\frac{11}{35}A$����A����
B����Ϊ�����ѹ��ԭ��Ȧa��b�������ӽ���������䣬������A1ʾ����������С���������빦����������С�������ѹ����û��������ʧ����ʾ������ʼ���ѹ��V2�͵�����A2ʾ���ij˻�ҲӦ��������С����B��ȷ��
C�������ѹ��ԭ��Ȧa��b���˽����ҽ����ѹu=220$\sqrt{2}$sin100��t��V����ԭ������Ȧ��������n1��n2=10��1������$\frac{{U}_{1}}{{U}_{2}}=\frac{{n}_{1}}{{n}_{2}}$�ã�����Ȧ���˵ĵ�ѹΪ��${U}_{2m}=\frac{{n}_{2}}{{n}_{1}}{U}_{1m}=\frac{1}{10}��220\sqrt{2}V=22\sqrt{2}V$��ѹ����ʾ��Ϊ��Чֵ�����Ե�ѹ��V1��ʾ��Ϊ��${U}_{V1}={U}_{2}=\frac{22\sqrt{2}}{\sqrt{2}}V=22V$�����������������ѹ���䣬���Ե�ѹ��V1��ʾ�����䣬��C����D������A�������֪��ͨ��R2�ĵ�����������С������P=I2R��֪��ֵ����R2���ĵĵ繦����������С����D����
��ѡ��B��
���� �������ڱ�ѹ���Ķ�̬�������⣬˼·���Ȳ��֣������壬�ٲ��֣�����Ĺؼ��Ǹ��ݲ�����·�ص�ã�$R=\frac{��4+x����8-x��}{4+8}=\frac{��4+x����8-x��}{12}$$��\frac{��\frac{4+x+8-x}{2}��^{2}}{12}=3��$�����ҽ���4+x=8-x����x=2��ʱȡ�Ⱥţ��������Ż�����ͷ���ƹ��̣���Ч�����ȼ�С������Ȼ���ٸ��ݱ�ѹ����ѹ��ϵ��ŷķ���ɵȽ�����⣮

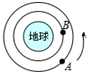
| A�� | B���DZ�A������������С | |
| B�� | A������ͼʾλ�ü��ٺ��п��ܻ�ײ��B���� | |
| C�� | A���ǵ������ٶ�һ��С�ڵ���ĵ�һ�����ٶ� | |
| D�� | ����ͨ��A���ǵ��������ں��������������������������� |
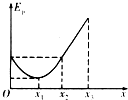 һ�����������ֻ�ڵ糡����������x�������˶����������EP��λ��x�仯�Ĺ�ϵ��ͼ��ʾ������O��x2���ǶԳƵ����ߣ�x2��x3��ֱ�߶Σ��������ж���ȷ���ǣ�������
һ�����������ֻ�ڵ糡����������x�������˶����������EP��λ��x�仯�Ĺ�ϵ��ͼ��ʾ������O��x2���ǶԳƵ����ߣ�x2��x3��ֱ�߶Σ��������ж���ȷ���ǣ�������| A�� | x1���糡ǿ����� | |
| B�� | x2��x3������ǿ�糡 | |
| C�� | x1��x2��x3�����Ʀ�1����2����3�Ĺ�ϵΪ��1����2����3 | |
| D�� | ������O��x2�����ȱ����˶���x2��x3��������ֱ���˶� |
| A�� | �����ķ����ݳ����� | |
| B�� | Ӳ����Ư����ˮ���� | |
| C�� | ����ˮ�еĺ�īˮ�ܿ�ɢ�� | |
| D�� | ����ȫʧ�صĻ����£��ۻ��Ľ����������ɱ������� |
| A�� | ���崦��ƽ��״̬ʱ���ܵĺ���һ��Ϊ�� | |
| B�� | �������ܵĺ���Ϊ��ʱ��һ������ƽ��״̬ | |
| C�� | �������ܵĺ���Ϊ��ʱһ�����ھ�ֹ״̬ | |
| D�� | ���崦�ھ�ֹ״̬ʱ������һ��Ϊ�� |
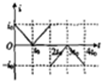
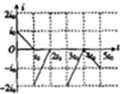
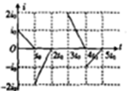
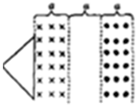 ��ͼ��ʾ��������ǿ�ų�����Ŀ��Ⱦ�Ϊa���м��ų�����Ŀ���ҲΪa����ǿ�ų�����ĴŸ�Ӧǿ�ȴ�С��ȣ������෴������б�߳�Ϊ$\sqrt{2}$a�ĵ���ֱ�������ε��߿�ͼʾλ�ÿ�ʼ��ˮƽ���ҵĺ㶨�ٶȴ�Խ�ó����������߿�����ʱ�뷽��Ϊ������������ͼ������ȷ�����ù����߿��и�Ӧ����i��ʱ��t�Ĺ�ϵ���ǣ�������
��ͼ��ʾ��������ǿ�ų�����Ŀ��Ⱦ�Ϊa���м��ų�����Ŀ���ҲΪa����ǿ�ų�����ĴŸ�Ӧǿ�ȴ�С��ȣ������෴������б�߳�Ϊ$\sqrt{2}$a�ĵ���ֱ�������ε��߿�ͼʾλ�ÿ�ʼ��ˮƽ���ҵĺ㶨�ٶȴ�Խ�ó����������߿�����ʱ�뷽��Ϊ������������ͼ������ȷ�����ù����߿��и�Ӧ����i��ʱ��t�Ĺ�ϵ���ǣ�������