题目内容
4.某天文台测得一颗卫星绕某行星做匀速圆周运动的轨道半径为r,周期为T,已知万有引力常量为G.求:(1)该卫星绕行星运动的向心加速度多大?
(2)该行星的质量是多少?
分析 根据圆周运动向心加速度公式求出向心加速度的大小.根据万有引力提供向心力求出行星的质量.
解答 解:(1)测得一颗卫星绕某行星做匀速圆周运动的轨道半径为r,周期为T,
根据圆周运动向心加速度公式得
a=$\frac{{4π}^{2}r}{{T}^{2}}$
(2)根据万有引力提供向心力得
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}r}{{T}^{2}}$
M=$\frac{{{4π}^{2}R}^{3}}{{GT}^{2}}$,
答:(1)该卫星绕行星运动的向心加速度是$\frac{{4π}^{2}r}{{T}^{2}}$;
(2)该行星的质量是$\frac{{{4π}^{2}R}^{3}}{{GT}^{2}}$.
点评 解决本题的关键掌握向心加速度与轨道半径和周期的关系,以及掌握万有引力提供向心力这一理论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.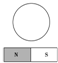 如图所示,在纸面内放有一个条形磁铁和一个圆形线圈(位于磁铁正中央),下列情况中能使线圈中产生感应电流的是( )
如图所示,在纸面内放有一个条形磁铁和一个圆形线圈(位于磁铁正中央),下列情况中能使线圈中产生感应电流的是( )
 如图所示,在纸面内放有一个条形磁铁和一个圆形线圈(位于磁铁正中央),下列情况中能使线圈中产生感应电流的是( )
如图所示,在纸面内放有一个条形磁铁和一个圆形线圈(位于磁铁正中央),下列情况中能使线圈中产生感应电流的是( )| A. | 将磁铁在纸面内向上平移 | |
| B. | 将磁铁在纸面内向右平移 | |
| C. | 将磁铁绕垂直纸面的轴转动 | |
| D. | 将磁铁的N极转向纸外,S极转向纸内 |
12.火车转弯时,为使车轮对内外轨道皆无侧向压力,需要按规定的速率转弯.火车提速后,仍在原轨道上转弯,此时( )
| A. | 轮缘对外轨有侧压力 | B. | 轮缘对内轨有侧压力 | ||
| C. | 轮缘对内、外轨都有侧压力 | D. | 轮缘对内、外轨都无侧压力 |
19.物体做曲线运动时,下列说法正确的是( )
| A. | 速度的大小可以不变而方向不断变化 | |
| B. | 速度的大小和方向都不变 | |
| C. | 速度的方向不变而大小不断变化 | |
| D. | 速度不变而加速度不断变化 |
16.电磁感应现象揭示了电和磁之间的内在联系,根据这一发现,发明了许多电器设备.下列用电器中,没有利用电磁感应原理的是( )
| A. | 电吹风 | B. | 日光灯镇流器 | C. | 变压器 | D. | 白炽灯泡 |
16. 如图所示,轻杆上紧密穿有质量相等的A、B两小球,将轻杆拉离竖直位置一定角度后由静止释放,则在两球向下摆动过程中,下列做功情况的叙述,正确的是( )
如图所示,轻杆上紧密穿有质量相等的A、B两小球,将轻杆拉离竖直位置一定角度后由静止释放,则在两球向下摆动过程中,下列做功情况的叙述,正确的是( )
 如图所示,轻杆上紧密穿有质量相等的A、B两小球,将轻杆拉离竖直位置一定角度后由静止释放,则在两球向下摆动过程中,下列做功情况的叙述,正确的是( )
如图所示,轻杆上紧密穿有质量相等的A、B两小球,将轻杆拉离竖直位置一定角度后由静止释放,则在两球向下摆动过程中,下列做功情况的叙述,正确的是( )| A. | 杆OA对A球做正功 | B. | 杆AB对B球不做功 | C. | 杆AB对A球做负功 | D. | 杆AB对B球做正功 |
 质量为M的楔形物块上有圆弧轨道,静止在水平面上.质量为m的小球以速度v1向物块运动.不计一切摩擦,圆弧小于90°且足够长.求物块的最终速度v和小球能上升到的最大高度H.
质量为M的楔形物块上有圆弧轨道,静止在水平面上.质量为m的小球以速度v1向物块运动.不计一切摩擦,圆弧小于90°且足够长.求物块的最终速度v和小球能上升到的最大高度H. 一个质量为m=0.5×10-4㎏,带有电量q=5×10-4C的小滑块放置在倾角为α=30°光滑的斜面上(假设物块的电量保持不变),斜面置于B=0.5T的匀强磁场中,磁场方向垂直纸面向里,如图所示,小滑块由静止开始沿斜面下滑,设斜面足够长,小滑块滑至某一位置时,要离开斜面.求:
一个质量为m=0.5×10-4㎏,带有电量q=5×10-4C的小滑块放置在倾角为α=30°光滑的斜面上(假设物块的电量保持不变),斜面置于B=0.5T的匀强磁场中,磁场方向垂直纸面向里,如图所示,小滑块由静止开始沿斜面下滑,设斜面足够长,小滑块滑至某一位置时,要离开斜面.求: