题目内容
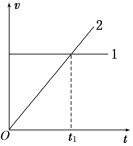
【题目】带有1/4光滑圆弧轨道质量为M的滑车静止置于光滑水平面上，如图所示，一质量也为M的小球以速度v0水平冲上滑车，到达某一高度后，小球又返回车的左端，则
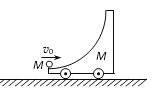
A. 小球以后将向左做平抛运动
B. 小球将做自由落体运动
C. 此过程小球对小车做的功为
D. 小球在弧形槽上升的最大高度为
【答案】BC
【解析】
试题小球和小车组成的系统，在水平方向上动量守恒，小球越过圆弧轨道后，在水平方向上与小车的速度相同，返回时仍然落回轨道，根据动量守恒定律判断小球的运动情况．对小车，运用动能定理求小球对小车做的功．当小球与小车的速度相同时，小球上升到最大高度，由动量守恒定律和机械能守恒定律结合求解最大高度．
小球滑上滑车，又返回，到离开滑车的整个过程中，系统水平方向动量守恒．选取向右为正方向，由动量守恒定律得：
，由机械能守恒定律得：
，解得：
，即小球在水平方向上速度为零，离开后做自由落体运动，故B正确A错误；对小车，运用动能定理得：小球对小车做的功
，故C正确；当小球与小车的速度相同时，小球上升到最大高度，设共同速度为v．规定向右为正方向，运用动量守恒定律得
，根据能量守恒定律得，有：
，代入数据得
，D错误．
【题目】某同学用如图1所示的实验装置探究小车动能变化与合外力对它所做功的关系．图中A为小车，连接在小车后面的纸带穿过打点计时器B的限位孔，它们均置于水平放置的一端带有定滑轮的足够长的木板上，C为弹簧测力计，不计绳与滑轮的摩擦．实验时，先接通电源再松开小车，打点计时器在纸带上打下一系列点．
①该同学在一条比较理想的纸带上，从点迹清楚的某点开始记为O点，顺次选取5个点，分别测量这5个点到O之间的距离，并计算出它们与O点之间的速度平方差△V2（△V2="V"2﹣V02），填入表：
点迹 | s/cm | △v2/m2s2 |
O | / | / |
1 | 1．60 | 0．04 |
2 | 3．60 | 0．09 |
3 | 6．00 | 0．15 |
4 | 7．00 | 0．18 |
5 | 9．20 | 0．23 |
若测出小车质量为0．2kg，结合如图2的图象可求得小车所受合外力的大小为___N
②本实验中是否必须满足小桶（含内部沙子）的质量远小于小车的质量________（填是或否）
③若该同学通过计算发现小车所受合力小于弹簧测力计读数，明显超出实验误差的正常范围．你认为主要原因是________．
【题目】采用让重物自由下落的方法验证机械能守恒定律,实验装置如图所示:现有的器材为:带铁夹的铁架台、电火花打点计时器、纸带、重锤.
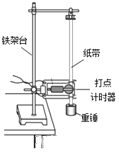
（1）需要测量物体由静止开始自由下落到某点时的瞬时速度v和下落高度h。某班同学利用实验得到的纸带,设计了以下四种测量方案,正确的是（_____）
A.用刻度尺测出物体下落的高度h,并测出下落时间t,通过v=gt计算出瞬时速度v
B.用刻度尺测出物体下落的高度h,并通过
计算出瞬时速度v
C.根据做匀变速直线运动时纸带上某点的瞬时速度,等于这点前后相邻两点间的平均速度,计算出瞬时速度v,并通过
计算出高度h。
D.用刻度尺测出物体下落的高度h,根据做匀变速直线运动时纸带上某点的瞬时速度,等于这点前后相邻两点间的平均速度,计算出瞬时速度v。
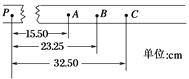
（2）甲同学从打出的纸带中选出一条理想的纸带,如图所示。选取纸带上连续打出的5个点A、B、C、D、E,测出A点与起始点O的距离为s0,点A、C间的距离为s1,点C、E间的距离为s2。已知重锤的质量为m,打点计时器所接交流电的频率为f,当地的重力加速度为g。从起始点O开始到打下C点的过程中,重锤重力势能的减小量为△EP=__________,重锤动能的增加量为△EK=__________。在误差充许的范围内,如果△EP=△EK,则可验证机械能守恒。
（3）乙同学经正确操作得到打点纸带,在纸带后段每两个计时间隔取一个计数点,依次为1、2、3、4、5、6、7,测量各计数点到起始点的距离h,并正确求出打相应点时的速度v。各计数点对应的数据见下表:
计数点 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
h/m | 0.124 | 0.194 | 0.279 | 0.380 | 0.497 | 0.630 | 0.777 |
v/(m·s-1) | 1.94 | 2.33 | 2.73 | 3.13 | 3.50 | ||
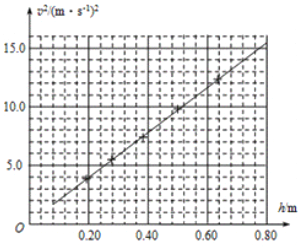
v2/(m2·s-2) | 3.76 | 5.43 | 7.45 | 9.80 | 12.25 |
他在如图所示的坐标中,描点作出v2-h图线。由图线可知,重锤下落的加速度g′=__________m/s2(保留三位有效数字);若当地的重力加速度g=9.80m/s2,如果在误差允许的范围内g′=__________,则可验证机械能守恒。
