题目内容
1. 如图所示,人造卫星A、B在同一平面内绕地心O做匀速圆周运动.已知A,B连线在A、O连线间的夹角最大为θ,则卫星A,B的角速度之比$\frac{ω{\;}_{A}}{ω{\;}_{B}}$等于( )
如图所示,人造卫星A、B在同一平面内绕地心O做匀速圆周运动.已知A,B连线在A、O连线间的夹角最大为θ,则卫星A,B的角速度之比$\frac{ω{\;}_{A}}{ω{\;}_{B}}$等于( )| A. | sin3θ | B. | $\sqrt{si{n}^{3}θ}$ | C. | $\frac{1}{si{n}^{3}θ}$ | D. | $\sqrt{\frac{1}{si{n}^{3}θ}}$ |
分析 根据题意知道AB连线与卫星B的运行轨道相切时,夹角θ最大,运用几何关系求出A、B轨道半径之比,由开普勒第三定律求出周期之比,即可得解.
解答 解:设A、B的轨道半径分别RA、RB.
据题卫星A、B连线与A、O连线间的夹角最大时,AB连线与卫星B的运行轨道应相切,如图:
根据几何关系有 RB=RAsinθ
根据开普勒第三定律有:$\frac{{R}_{A}^{3}}{{R}_{B}^{3}}$=$\frac{{T}_{A}^{2}}{{T}_{B}^{2}}$
又有角速度之比 $\frac{ω{\;}_{A}}{ω{\;}_{B}}$=$\frac{{T}_{B}}{{T}_{A}}$
联立解得 $\frac{ω{\;}_{A}}{ω{\;}_{B}}$=$\sqrt{si{n}^{3}θ}$
故选:B.
点评 能根据题目给出的信息分析视角最大时的半径特征,在圆周运动中涉及几何关系求半径是一个基本功问题.

练习册系列答案
相关题目
12. 如图a所示为某种检测油箱中油深度的油量计,它是由许多透明等厚的薄塑料片叠合而成.每个薄片的形状如图b所示,其底部尖角为直角,且两腰相等.薄片的长度从很短到接近油箱底部不等.把这一油量计固定在油箱盖上,通过油箱盖的矩形窗口可以看到油量计的上端面.把油量计竖直插入油箱,从上端面明暗分界线的位置可以知道油的深度.下列有关油量计上端面的“明暗”说法正确的是( )
如图a所示为某种检测油箱中油深度的油量计,它是由许多透明等厚的薄塑料片叠合而成.每个薄片的形状如图b所示,其底部尖角为直角,且两腰相等.薄片的长度从很短到接近油箱底部不等.把这一油量计固定在油箱盖上,通过油箱盖的矩形窗口可以看到油量计的上端面.把油量计竖直插入油箱,从上端面明暗分界线的位置可以知道油的深度.下列有关油量计上端面的“明暗”说法正确的是( )
 如图a所示为某种检测油箱中油深度的油量计,它是由许多透明等厚的薄塑料片叠合而成.每个薄片的形状如图b所示,其底部尖角为直角,且两腰相等.薄片的长度从很短到接近油箱底部不等.把这一油量计固定在油箱盖上,通过油箱盖的矩形窗口可以看到油量计的上端面.把油量计竖直插入油箱,从上端面明暗分界线的位置可以知道油的深度.下列有关油量计上端面的“明暗”说法正确的是( )
如图a所示为某种检测油箱中油深度的油量计,它是由许多透明等厚的薄塑料片叠合而成.每个薄片的形状如图b所示,其底部尖角为直角,且两腰相等.薄片的长度从很短到接近油箱底部不等.把这一油量计固定在油箱盖上,通过油箱盖的矩形窗口可以看到油量计的上端面.把油量计竖直插入油箱,从上端面明暗分界线的位置可以知道油的深度.下列有关油量计上端面的“明暗”说法正确的是( )| A. | 光线在塑料和油的界面处发生折射现象,故人看起来是暗的 | |
| B. | 光线在塑料和油的界面处发生全反射现象,故人看起来是明亮的 | |
| C. | 光线在塑料和空气的界面处发生全反射现象,故人看起来是明亮的 | |
| D. | 光线在塑料和空气的界面处发生折射现象,故人看起来是暗的 |
12.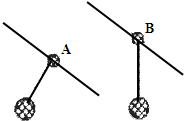 两倾斜的平行滑杆上分别套A、B两圆环,两环上均用细线悬吊着物体,如图所示.当它们都沿滑杆向下滑动时(环、物保持相对静止),A的悬线与杆垂直,B的悬线竖直向下,则( )
两倾斜的平行滑杆上分别套A、B两圆环,两环上均用细线悬吊着物体,如图所示.当它们都沿滑杆向下滑动时(环、物保持相对静止),A的悬线与杆垂直,B的悬线竖直向下,则( )
 两倾斜的平行滑杆上分别套A、B两圆环,两环上均用细线悬吊着物体,如图所示.当它们都沿滑杆向下滑动时(环、物保持相对静止),A的悬线与杆垂直,B的悬线竖直向下,则( )
两倾斜的平行滑杆上分别套A、B两圆环,两环上均用细线悬吊着物体,如图所示.当它们都沿滑杆向下滑动时(环、物保持相对静止),A的悬线与杆垂直,B的悬线竖直向下,则( )| A. | A环与杆有摩擦力 | B. | B环与杆无摩擦力 | ||
| C. | A环做的是匀速运动 | D. | B环做的是匀速运动 |
16.如图所示,图甲为一列简谐横波t=0.50s时的波形图象,P点是距平衡位置2.5cm的质点,图乙是Q点的振动图象,以下说法正确的是( )


| A. | 0.05s时质点Q具有最大的加速度和位移 | |
| B. | 0.05s时质点P的速度正在减小,加速度正在增大 | |
| C. | 这列简谐横波的波速为15m/s | |
| D. | 这列波的传播方向为+x方向 | |
| E. | 从0.60s到0.90s,质点P通过的路程为30cm |
10. 如图所示,是以弹簧振子,设向右方向为正,O为平衡位置,则( )
如图所示,是以弹簧振子,设向右方向为正,O为平衡位置,则( )
 如图所示,是以弹簧振子,设向右方向为正,O为平衡位置,则( )
如图所示,是以弹簧振子,设向右方向为正,O为平衡位置,则( )| A. | A→O位移为负值,速度为正值 | B. | O→A′时,位移为正值,加速度为负值 | ||
| C. | A′→O时,位移为负值,速度为负值 | D. | O→A时,位移为负值,加速度为正值 |
11. a、b、c三个物体在同一条直线上运动,其位移时间图象中,图线c是一条x=0.4t2的抛物线.有关这三个物体在0~5s内的运动,下列说法正确的是( )
a、b、c三个物体在同一条直线上运动,其位移时间图象中,图线c是一条x=0.4t2的抛物线.有关这三个物体在0~5s内的运动,下列说法正确的是( )
 a、b、c三个物体在同一条直线上运动,其位移时间图象中,图线c是一条x=0.4t2的抛物线.有关这三个物体在0~5s内的运动,下列说法正确的是( )
a、b、c三个物体在同一条直线上运动,其位移时间图象中,图线c是一条x=0.4t2的抛物线.有关这三个物体在0~5s内的运动,下列说法正确的是( )| A. | a物体做匀加速直线运动 | |
| B. | c物体做匀加速直线运动 | |
| C. | t=5 s时,a物体速度最大 | |
| D. | a、b两物体都做匀速直线运动,且速度相同 |

 如图所示,实线和虚线分别是沿x轴传播的一列简谐横波在t=0和t=0.06s时刻的波形图.已知在t=0时刻,x=1.5m处的质点向y轴正方向运动.
如图所示,实线和虚线分别是沿x轴传播的一列简谐横波在t=0和t=0.06s时刻的波形图.已知在t=0时刻,x=1.5m处的质点向y轴正方向运动. 一质量为m的小车静止在光滑的水平面上,车厢长L=2m.在车厢底板上的正中位置放置一个质量也为m的物块,如图所示.若给物块一个冲量,使之以v=10m/s的初速度向右运动,已知物块与车厢底部间的动摩擦因数μ=0.2,物块与车厢壁的碰撞时完全弹性碰撞,且水平面足够大,物块可视为质点.(取g=10m/s2)
一质量为m的小车静止在光滑的水平面上,车厢长L=2m.在车厢底板上的正中位置放置一个质量也为m的物块,如图所示.若给物块一个冲量,使之以v=10m/s的初速度向右运动,已知物块与车厢底部间的动摩擦因数μ=0.2,物块与车厢壁的碰撞时完全弹性碰撞,且水平面足够大,物块可视为质点.(取g=10m/s2)