题目内容
14. 如图,木块与木板通过弹簧连接,木块的质量为m,木板的质量为M,弹簧的劲度系数为k,当弹簧伸长x时,木块刚好相对木板静止,水平面光滑.现给木板一水平向右的力F,要使木块不相对木板滑动( )
如图,木块与木板通过弹簧连接,木块的质量为m,木板的质量为M,弹簧的劲度系数为k,当弹簧伸长x时,木块刚好相对木板静止,水平面光滑.现给木板一水平向右的力F,要使木块不相对木板滑动( )| A. | 拉力F应小于kx | B. | 拉力F应小于2kx | ||
| C. | 不可能相对滑动 | D. | 拉力F应小于$\frac{2(M+m)kx}{m}$ |
分析 根据木块受到的最大静摩擦力求的木块的最大加速度,整体有牛顿第二定律求的拉力
解答 解:开始弹簧伸长,m与M之间的最大摩擦力为f=kx,在F的作用下它们一起加速度运动,要使m相等M静止,则弹簧的弹力只能是kx
而m与M之间的最大静摩擦力为kx,当M的加速度太大时,m相对M要向左运动,此时m受到的摩擦力方向水平向右,
故m的最大允许加速度为:kx+f=ma,解得a=$\frac{2kx}{m}$
因此要保持m、M相对静止,则M、m的最大加速度只能是m
对整体:F=(M+m)a=$\frac{2(M+m)kx}{m}$
故选:D
点评 本题主要考查了临界加速度的求法,然后根据整体法求的拉力

练习册系列答案
相关题目
18. 如图表示一个电场中a、b、c、d四点分别引入试探电荷,测得试探电荷所受的力F与电荷量q之间的函数关系,如图所示,下列说法正确的是( )
如图表示一个电场中a、b、c、d四点分别引入试探电荷,测得试探电荷所受的力F与电荷量q之间的函数关系,如图所示,下列说法正确的是( )
 如图表示一个电场中a、b、c、d四点分别引入试探电荷,测得试探电荷所受的力F与电荷量q之间的函数关系,如图所示,下列说法正确的是( )
如图表示一个电场中a、b、c、d四点分别引入试探电荷,测得试探电荷所受的力F与电荷量q之间的函数关系,如图所示,下列说法正确的是( )| A. | 该电场是匀强电场 | |
| B. | a、b、c、d四点场强大小关系是:Ed>Ea>Eb>Ec | |
| C. | 这四点场强大小关系是:Ea>Eb>Ec>Ed,场源是正电荷 | |
| D. | 无法判断a、b、c、d四点场强大小关系 |
19.下列各组物理量全部为矢量的一组是( )
| A. | 速度、加速度、位移 | B. | 速度、质量、位移 | ||
| C. | 加速度、质量、时间 | D. | 力、功、温度 |
19. 如图所示,在电梯的水平地板上放置一质量为m的物体,电梯竖直向上匀速运动高度为H的过程中,下列说法正确的是( )
如图所示,在电梯的水平地板上放置一质量为m的物体,电梯竖直向上匀速运动高度为H的过程中,下列说法正确的是( )
 如图所示,在电梯的水平地板上放置一质量为m的物体,电梯竖直向上匀速运动高度为H的过程中,下列说法正确的是( )
如图所示,在电梯的水平地板上放置一质量为m的物体,电梯竖直向上匀速运动高度为H的过程中,下列说法正确的是( )| A. | 重力对物体做的功等于mgH | |
| B. | 电梯地板对物体的支持力做的功等于0 | |
| C. | 电梯地板对物体的支持力做的功等于mgH | |
| D. | 合力对物体做的功等于0 |
3. 如图所示,水平桌面上平放有一堆卡片,每一张卡片的质量均为m.用一手指以竖直向下的力压第1张卡片,并以一定速度向右移动手指,确保第1张卡片与第2张卡片之间有相对滑动.设最大静摩擦力与滑动摩擦力相同,手指与第1张卡片之间的动摩擦因数为μ1,卡片之间、卡片与桌面之间的动摩擦因数均为μ2,且有μ1>μ2,则下列说法正确的是( )
如图所示,水平桌面上平放有一堆卡片,每一张卡片的质量均为m.用一手指以竖直向下的力压第1张卡片,并以一定速度向右移动手指,确保第1张卡片与第2张卡片之间有相对滑动.设最大静摩擦力与滑动摩擦力相同,手指与第1张卡片之间的动摩擦因数为μ1,卡片之间、卡片与桌面之间的动摩擦因数均为μ2,且有μ1>μ2,则下列说法正确的是( )
 如图所示,水平桌面上平放有一堆卡片,每一张卡片的质量均为m.用一手指以竖直向下的力压第1张卡片,并以一定速度向右移动手指,确保第1张卡片与第2张卡片之间有相对滑动.设最大静摩擦力与滑动摩擦力相同,手指与第1张卡片之间的动摩擦因数为μ1,卡片之间、卡片与桌面之间的动摩擦因数均为μ2,且有μ1>μ2,则下列说法正确的是( )
如图所示,水平桌面上平放有一堆卡片,每一张卡片的质量均为m.用一手指以竖直向下的力压第1张卡片,并以一定速度向右移动手指,确保第1张卡片与第2张卡片之间有相对滑动.设最大静摩擦力与滑动摩擦力相同,手指与第1张卡片之间的动摩擦因数为μ1,卡片之间、卡片与桌面之间的动摩擦因数均为μ2,且有μ1>μ2,则下列说法正确的是( )| A. | 任意两张卡片之间均可能发生相对滑动 | |
| B. | 上一张卡片受到下一张卡片的摩擦力一定向左 | |
| C. | 第1张卡片受到手指的摩擦力向左 | |
| D. | 最后一张卡片受到水平桌面的摩擦力向右 |
4.一起重机的钢绳由静止开始匀加速提起质量为m1的重物,当重物的速度为vl时,起重机的输出功率达到最大值P;若由静止开始以相同加速度匀加速提起质量为m2(m2>m1)的重物,当重物的速度为v2时,起重机的输出功率达到最大值P.重力加速度为g,不计空气阻力.则两个过程中,下列说法正确的是( )
| A. | 钢绳较大的拉力为$\frac{P}{{v}_{1}}$ | |
| B. | 钢绳较大的拉力为$\frac{P}{{v}_{2}}$+mg | |
| C. | 两物体质量之比为$\frac{{m}_{1}}{{m}_{2}}$=$\frac{{v}_{2}}{{v}_{1}}$ | |
| D. | 重物m1做匀加速运动的时间为$\frac{{m}_{1}{{v}_{1}}^{2}}{P+{m}_{1}g{v}_{1}}$ |
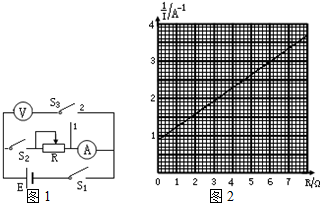 某同学设计了如图1所示的电路来测量某一电源的电动势和内电阻,图中
某同学设计了如图1所示的电路来测量某一电源的电动势和内电阻,图中 为内阻可以忽略的电流表,
为内阻可以忽略的电流表, 为电压表,R是滑动变阻器,三个开关都处于断开状态.
为电压表,R是滑动变阻器,三个开关都处于断开状态. 由于接触不良而不能使用,该同学被迫将滑线变阻器换成电阻箱重新实验,他将测得的多组I-R数据绘制成图2所示的图线,由图可知待测电源的电动势和内电阻各是多少?
由于接触不良而不能使用,该同学被迫将滑线变阻器换成电阻箱重新实验,他将测得的多组I-R数据绘制成图2所示的图线,由图可知待测电源的电动势和内电阻各是多少? 如图所示,V形转盘可绕竖直中心轴OO′转动,V形转盘的侧面与竖直转轴间的夹角均为α=53°,盘上放着质量为1kg的物块A,物块A用长为1m的细线与固定在转盘中心O处的力传感器相连.物块和传感器的大小均可忽略不计,细线能承受的最大拉力为8N,A与转盘间的动摩擦因数μ为1.5,且可认为最大静摩擦力等于滑动摩擦力.转盘转动时,细线一直伸直,当转盘以不同的角速度匀速转动时,传感器上就会显示相应的读数F.
如图所示,V形转盘可绕竖直中心轴OO′转动,V形转盘的侧面与竖直转轴间的夹角均为α=53°,盘上放着质量为1kg的物块A,物块A用长为1m的细线与固定在转盘中心O处的力传感器相连.物块和传感器的大小均可忽略不计,细线能承受的最大拉力为8N,A与转盘间的动摩擦因数μ为1.5,且可认为最大静摩擦力等于滑动摩擦力.转盘转动时,细线一直伸直,当转盘以不同的角速度匀速转动时,传感器上就会显示相应的读数F.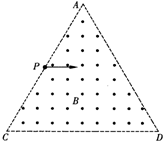 如图所示,在边长为L的等边三角形ACD区域内,存在磁感应强度B、方向垂直纸面向外的匀强磁场.现有一束质量为m,电荷量为+q的带电粒子,以某一速度从AC边中点P、平行于CD边垂直磁场射入,粒子的重力可忽略不计.
如图所示,在边长为L的等边三角形ACD区域内,存在磁感应强度B、方向垂直纸面向外的匀强磁场.现有一束质量为m,电荷量为+q的带电粒子,以某一速度从AC边中点P、平行于CD边垂直磁场射入,粒子的重力可忽略不计.