题目内容
 (2013?湖北模拟)如图所示,质量为m的小物块Q(大小不计),位于质量为M的平板P的左端,系统原来静 止在光滑水平面上.一不可伸长的轻质细绳长为R,一端悬于Q正上方高为R处,另一端系一质量也为m的 小球.(大小不计),今将小球拉至悬线与竖直方向成600角的位置,由静止释放,小球到达最低点时与Q发生碰撞,且碰撞时间极短,无能 量损失.已知Q刚好不离开平板车,Q与P之间的动摩擦因数为u,M:m=4:1,重力加速度为g求:
(2013?湖北模拟)如图所示,质量为m的小物块Q(大小不计),位于质量为M的平板P的左端,系统原来静 止在光滑水平面上.一不可伸长的轻质细绳长为R,一端悬于Q正上方高为R处,另一端系一质量也为m的 小球.(大小不计),今将小球拉至悬线与竖直方向成600角的位置,由静止释放,小球到达最低点时与Q发生碰撞,且碰撞时间极短,无能 量损失.已知Q刚好不离开平板车,Q与P之间的动摩擦因数为u,M:m=4:1,重力加速度为g求:①小物块Q最终的速度大小;
②平板车P的长度.
分析:小球到达最低点时与Q的碰撞时间极短,且无能量损失,满足动量守恒的条件且能量守恒.小物块Q在平板车P上滑动的过程中,二者相互作用,动量守恒,部分动能转化为内能.
解答:解:①小球由静止摆到最低点的过程中,有
mgR(1-cos60°)=
mv02
v0=
小球与物块Q相撞时,没有能量损失,动量守恒,机械能守恒,
二者交换速度,即小球静止
且vQ=v0=
设小物块最终的速度为v
由动量守恒定律有mvQ=(M+m)v
代入数据解得v=
②设平板车长度为L
由能量转化和守恒定律有:
μmgL=
mvQ2-
(M+m)v2
代入数据解得:L=
答:①小物块Q最终的速度大小
;
②平板车P的长度为
.
mgR(1-cos60°)=
| 1 |
| 2 |
v0=
| gR |
小球与物块Q相撞时,没有能量损失,动量守恒,机械能守恒,
二者交换速度,即小球静止
且vQ=v0=
| gR |
设小物块最终的速度为v
由动量守恒定律有mvQ=(M+m)v
代入数据解得v=
| 1 |
| 5 |
| gR |
②设平板车长度为L
由能量转化和守恒定律有:
μmgL=
| 1 |
| 2 |
| 1 |
| 2 |
代入数据解得:L=
| 2R |
| 5μ |
答:①小物块Q最终的速度大小
| 1 |
| 5 |
| gR |
②平板车P的长度为
| 2R |
| 5μ |
点评:逐一分析物体间的相互作用过程,分析得到物体间相互作用时满足的规律:动量守恒、能量守恒等,进而求出要求的物理量.

练习册系列答案
相关题目
 (2013?湖北模拟)在用打点计时器验证机械能守恒定律的实验中,使质量为m=1.00kg的重物自由下落,打点计时器在纸带上打出一系列的点,选取一条符合实验要求的纸带如图所示.O为第一个点,A、B、C为从合适位置开始选取连续点中的三个点.已知打点计时器每隔0.02s打一个点,当地的重力加速度为g=9.80m/s2,那么:
(2013?湖北模拟)在用打点计时器验证机械能守恒定律的实验中,使质量为m=1.00kg的重物自由下落,打点计时器在纸带上打出一系列的点,选取一条符合实验要求的纸带如图所示.O为第一个点,A、B、C为从合适位置开始选取连续点中的三个点.已知打点计时器每隔0.02s打一个点,当地的重力加速度为g=9.80m/s2,那么: (2013?湖北模拟)如图所示,某同学骑电动车以 10m/s的速度匀速驶向路口,当行驶至距路口停车线20m处时,绿灯还有3s熄灭.而该同学在绿灯熄灭时刚好停在停车线处,则该同学运动的v-t图象可能是( )
(2013?湖北模拟)如图所示,某同学骑电动车以 10m/s的速度匀速驶向路口,当行驶至距路口停车线20m处时,绿灯还有3s熄灭.而该同学在绿灯熄灭时刚好停在停车线处,则该同学运动的v-t图象可能是( )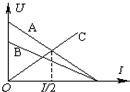 (2013?湖北模拟)如图所示,直线A为电源a的路端电压与电流的关系图象,直线B为电源b的路端电压与电流的关系图象,直线C为一个电阻R的两端电压与电流的关系图象.将这个电阻R分别接到a、b两电源上,那么( )
(2013?湖北模拟)如图所示,直线A为电源a的路端电压与电流的关系图象,直线B为电源b的路端电压与电流的关系图象,直线C为一个电阻R的两端电压与电流的关系图象.将这个电阻R分别接到a、b两电源上,那么( ) (2013?湖北模拟)一定质量的理想气体从状态A变化到状态B,再变化到状态C,其状态变化过程的p-V图象如图所示.已知该气体在状态A时的温度为27℃.则:
(2013?湖北模拟)一定质量的理想气体从状态A变化到状态B,再变化到状态C,其状态变化过程的p-V图象如图所示.已知该气体在状态A时的温度为27℃.则: (2013?湖北模拟)如图所示,实线和虚线分别是沿x轴传播的一列简谐横波在t=0和t=0.06s时刻的波形图.已知在t=0时刻,x=1.5m处的质点向y轴正方向运动.
(2013?湖北模拟)如图所示,实线和虚线分别是沿x轴传播的一列简谐横波在t=0和t=0.06s时刻的波形图.已知在t=0时刻,x=1.5m处的质点向y轴正方向运动.