题目内容
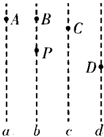 如图所示,a、b、c、d为匀强电场中四个等势面,相邻等势面间距离为2cm,已知UAC=60V,求:
如图所示,a、b、c、d为匀强电场中四个等势面,相邻等势面间距离为2cm,已知UAC=60V,求:(1)电场强度是多大?
(2)设B点电势为零,求A、C、D、P点的电势.
(3)求将q=-1.0×10-10C的点电荷由A移到D电场力所做的功WAD.
(4)将q=2×10-10C的点电荷由B移到C,再经D最后回到P,电场力所做的功WBCDP.
分析:(1)电场线和等势面垂直,求出AC间的距离,根据E=
求出匀强电场的电场强度.
(2)求出B点与各点间的电势差,从而根据B点的电势求出A、C、D、P点的电势.
(3)求出AD间的电势差,根据WAD=qUAD求出电场力做功.
(4)抓住电场力做功与路径无关,找出两点间的电势差,即可求出电场力做功.
| U |
| d |
(2)求出B点与各点间的电势差,从而根据B点的电势求出A、C、D、P点的电势.
(3)求出AD间的电势差,根据WAD=qUAD求出电场力做功.
(4)抓住电场力做功与路径无关,找出两点间的电势差,即可求出电场力做功.
解答:解:(1)AC间的距离为4cm.
则E=
=
V/m=1500V/m.
故匀强电场的场强为1500V/m.
(2)根据A点的电势大于C点的电势,知电场强度的方向水平向右.
UAB=1500×0.02V=30V,因为φB=0,则φA=30V.
UBC=30V,则φC=-30V.UBD=60V,则φD=-60V.
P点与B点等电势,所以φp=0V.
故A、C、D、P点的电势分别为:30V、-30V、-60V、0V.
(3)UAD=φA-φD=90V
则WAD=qUAD=-1×10-10×90J=-9×10-9J.
故点电荷由A移到D电场力所做的功为-9×10-9J.
(4)B、P两点等电势,则B、P间的电势差为0,根据W=qU知,电场力做功为0.
故电场力所做的功WBCDP=0.
则E=
| UAC |
| d |
| 60 |
| 0.04 |
故匀强电场的场强为1500V/m.
(2)根据A点的电势大于C点的电势,知电场强度的方向水平向右.
UAB=1500×0.02V=30V,因为φB=0,则φA=30V.
UBC=30V,则φC=-30V.UBD=60V,则φD=-60V.
P点与B点等电势,所以φp=0V.
故A、C、D、P点的电势分别为:30V、-30V、-60V、0V.
(3)UAD=φA-φD=90V
则WAD=qUAD=-1×10-10×90J=-9×10-9J.
故点电荷由A移到D电场力所做的功为-9×10-9J.
(4)B、P两点等电势,则B、P间的电势差为0,根据W=qU知,电场力做功为0.
故电场力所做的功WBCDP=0.
点评:解决本题的关键知道等势面与电场线关系,掌握匀强电场的场强公式,以及电场力做功与电势差的关系.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目

 如图所示,a、b、c为电场中同一电场线上的三点,且b为ac的中点,a、c电势分别为φa=8V,φc=6V.下列叙述正确的是( )
如图所示,a、b、c为电场中同一电场线上的三点,且b为ac的中点,a、c电势分别为φa=8V,φc=6V.下列叙述正确的是( ) 如图所示,A、B、C、D是某匀强电场中的4个等势面,一个质子和一个α粒子(电荷量是质子的2倍,质量是质子的4倍)同时在A等势面从静止出发,向右运动,当到达D等势面时,下列说法正确的是( )
如图所示,A、B、C、D是某匀强电场中的4个等势面,一个质子和一个α粒子(电荷量是质子的2倍,质量是质子的4倍)同时在A等势面从静止出发,向右运动,当到达D等势面时,下列说法正确的是( ) 如图所示,a、b和c都是厚度均匀的平玻璃板,a和b、b和c之间的夹角都为α,一细光束由红光和蓝光组成,以入射角θ从O点射入a板,且射出c板后的两束单色光通过空气射在地面上P、Q两点,由此可知( )
如图所示,a、b和c都是厚度均匀的平玻璃板,a和b、b和c之间的夹角都为α,一细光束由红光和蓝光组成,以入射角θ从O点射入a板,且射出c板后的两束单色光通过空气射在地面上P、Q两点,由此可知( ) 如图所示,a、b、c是匀强电场中的直角三角形的三个顶点.已知a、b、c三点的电势分别为φa=8V、φb=-4V、φc=2V,
如图所示,a、b、c是匀强电场中的直角三角形的三个顶点.已知a、b、c三点的电势分别为φa=8V、φb=-4V、φc=2V,