题目内容
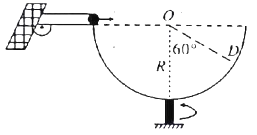
【题目】如图所示，在竖直平面内，有一半径为R的半圆形圆环绕着过最低点的竖直轴以角速度ω按逆时针方向(俯视)匀速转动，一玩具枪的枪口恰好位于圆环的一端每隔一定时间水平射出不同速度大小的小钢珠。当圆环转到图中位置时，某时刻射出的第一颗钢珠恰好击中圆环内壁的D点，同时枪射出第二颗钢珠，经过一定时间，第二颗钢珠又恰好击中D点，已知D点和圆心O的连线与竖直方向的夹角为60°，不计空气阻力，则（ ）
A. 第一、二颗钢珠离开枪口的速度之比为
B. 第一、二颗钢珠离开枪口的速度之比为
C. 小钢珠能够垂直击中D点
D. 圆环的最小角速度为
【答案】AD
【解析】小钢珠做平抛运动，对第一颗钢珠，竖直方向有：
；水平方向：
；当圆环至少转过半圆时，第二颗钢珠又击中D点，有：
；
；解得t1=t2；
，选项A正确，B错误；假设小钢珠能垂直击中D点，即D点的速度方向沿半径OD，根据平抛运动的规律可知“速度的反向延长线必过水平位移的中点”，可知假设错误，选项C错误；当圆环转过半圈，被第二颗钢珠击中时，圆环的角速度最小，有
，解得
，选项D正确；故选AD.
练习册系列答案
黄冈创优卷系列答案
相关题目
