题目内容
如图所示，质量为m、长为L的导体棒电阻为R，初始时静止于光滑的水平轨道上，电源电动势为E，内阻不计。匀强磁场的磁感应强度为B，其方向与轨道平面成θ角斜向上方，开关闭合后导体棒开始运动，则( )
| A．导体棒向左运动 |
B．开关闭合瞬间导体棒MN所受安培力为 |
C．开关闭合瞬间导体棒MN所受安培力为 |
D．开关闭合瞬间导体棒MN的加速度为 |
BD
解析试题分析：内阻不计则闭合回路电流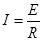
，而电流方向和磁场方向垂直，根据安培力的计算公式有
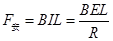选项B对C错。根据安培左手定则判断，安培力的方向斜向右下方，与竖直方向夹角为
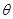，竖直方向重力支持力即安培力的竖直分力
相互平衡，而在水平方向，安培力的水平分力方向向右，导体棒将向右运动，选项A错。导体棒的加速度
，即
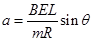选项D对。
考点：安培力
名校课堂系列答案如图，圆形区域内有垂直纸面的匀强磁场，三个完全相同的带电粒子a、b、c，以不同的速率对准圆心O沿着AO方向射入磁场，其运动轨迹如图。若带电粒子只受磁场力的作用，则下列说法正确的是 
| A．a粒子动能最大 |
| B．c粒子速率最大 |
| C．c粒子在磁场中运动时间最短 |
| D．它们做圆周运动的周期Ta<Tb<Tc |
如图所示，回旋加速器是加速带电粒子的装置，其核心部分是分别与高频交流电源两极相连接的两个D形金属盒，两盒间的狭缝中形成周期性变化的电场，使粒子在通过狭缝时都能得到加速，两D形金属盒处于垂直于盒底的匀强磁场中，D形盒半径为R．用该回旋加速器加速质子（质量数为1，核电荷数为1）时，匀强磁场的磁感应强度为B，高频交流电周期为T．（粒子通过狭缝的时间忽略不计）则
| A．质子在D形盒中做匀速圆周运动的周期为2T |
B．质子被加速后的最大速度可能超过 |
| C．质子被加速后的最大速度与加速电场的电压大小无关 |
| D．不改变B和T，该回旋加速器也能用于加速α粒子（质量数为4，核电荷数为2） |
如图所示，速度不同的同种带电粒子（重力不计）a、b沿半径AO方向进入一圆形匀强磁场区域，a，b两粒子的运动轨迹分别为AB和AC，则下列说法中正确的是
| A．a、b两粒子均带正电 |
| B．a粒子的速度比b粒子的速度大 |
| C．a粒子在磁场中的运动时间比b粒子长 |
| D．两粒子离开磁场时的速度反向延长线一定都过圆心O |
如图，在正方形abcd范围内，有方向垂直纸面向里的匀强磁场，两个电子以不同的速率，从a点沿ab方向垂直磁场方向射入磁场，其中甲电子从c点射出，乙电子从d点射出。不计重力，则甲、乙电子（ ）
| A．速率之比2:1 |
| B．在磁场中运行的周期之比1:2 |
| C．在正方形磁场中运行的时间之比1:2 |
| D．速度偏转角之比为1:2 |
如图所示，水平放置的直导线正下方有一只可以自由转动的小磁针，当导线中通过自左向右的电流时，小磁针N极的转动情况是
| A．垂直于纸面向里转 |
| B．垂直于纸面向外转 |
| C．在纸面内顺时针转 |
| D．在纸面内逆时针转 |
如图所示，三根通电长直导线P、Q、R互相平行，垂直纸面放置，其间距均为L，电流均为I，方向垂直纸面向里．已知电流为I的长直导线产生的磁场中，距导线r处的磁感应强度B=kI/r，其中k为常量．某时刻有一电荷量为q的带正电粒子经过原点O，速度大小为v，方向沿y轴正方向，该粒子此时所受磁场力为
A．方向垂直纸面向外，大小为 |
B．方向指向x轴正方向，大小为 |
C．方向垂直纸面向外，大小为 |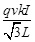
D．方向指向x轴正方向，大小为 |
∶1
B0