题目内容
【题目】为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞,某同学选取了两个体积相同、质量相差比较大的小球,按下述步骤做了实验:
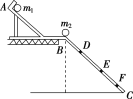
①用天平测出两小球的质量(分别为m1和m2,且m1>m2).
②按图示安装好实验器材,将斜槽AB固定在桌边,使槽的末端切线水平,将一斜面BC连接在斜槽末端.
③先不放小球m2,让小球m1从斜槽顶端A处由静止开始滚下,记下小球在斜面上的落点位置.
④将小球m2放在斜槽末端边缘处,让小球m1从斜槽顶端A处由静止开始滚下,使它们发生碰撞,分别记下小球m1和m2在斜面上的落点位置.
⑤用毫米刻度尺量出各个落点位置到斜槽末端点B的距离.图中D、E、F点是该同学记下小球在斜面上的落点位置,到B点的距离分别为LD、LE、LF.
根据该同学的实验,回答下列问题:
(1)在不放小球m2时,小球m1从斜槽顶端A处由静止开始滚下,m1的落点在图中的________点,把小球m2放在斜槽末端边缘处,小球m1从斜槽顶端A处由静止开始滚下,使它们发生碰撞,碰后小球m1的落点在图中的________点.
(2)若碰撞过程中,动量和机械能均守恒,不计空气阻力,则下列表达式中正确的有________.
A.m1LF=m1LD+m2LE
B.![]()
C.m1LE=m1LD+m2LF
D.LE=LF-LD
【答案】E D C
【解析】
(1)[1][2]小球m1从斜槽顶端A处由静止开始滚下,m1的落点在图中的E点,小球m1和小球m2相撞后,小球m2的速度增大,小球m1的速度减小,都做平抛运动,所以碰撞后m1球的落地点是D点,m2球的落地点是F点.
(2)[3]设斜面倾角为θ,小球落点到B点的距离为L,小球从B点抛出时速度为v,则竖直方向有Lsin θ=![]() gt2,水平方向有Lcos θ=vt,
gt2,水平方向有Lcos θ=vt,
解得
v=![]() =
=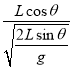 =
=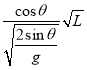
所以v∝![]() ,由题意分析得,只要满足m1v1=m2v2+m1v′1,把速度v代入整理得:
,由题意分析得,只要满足m1v1=m2v2+m1v′1,把速度v代入整理得:
![]()
说明两球碰撞过程中动量守恒;若两小球的碰撞是弹性碰撞,则碰撞前后机械能没有损失,则要满足关系式:
![]()
整理得m1LE=m1LD+m2LF,故C正确.ABD错误。