题目内容
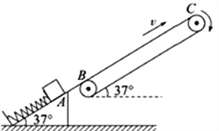
【题目】利用弹簧弹射和传送带传动装置可以将工件运送至高处．如图所示，已知传送轨道平面与水平方向成37°角，倾角也是37°的光滑斜面轨道固定于地面且与传送轨道良好对接，弹簧下端固定在斜面底端，工件与皮带间的动摩擦因数μ=0.25．传送带传动装置顺时针匀速转动的速度v=4m/s，两轮轴心相距L=5m，B、C分别是传送带与两轮的切点，轮缘与传送带之间不打滑．现将质量m=1kg的工件放在弹簧上，用力将弹簧压缩至A点后由静止释放，工件离开斜面顶端滑到传送带上的B点时速度v0=8m/s，AB间的距离s=1m．工件可视为质点，g取10m/s2（sin37°=0.6，cos37°=0.8）．求：
（1）弹簧的最大弹性势能；
（2）工件沿传送带上滑的时间；
（3）求工件在皮带上滑动的全过程中所产生的内能是多少．
【答案】（1）38J（2）1.5s（3）6J
【解析】（1）滑块从A到B过程，弹簧的弹性势能的减小等于滑块机械能的增加，根据机械能守恒定律，弹簧的最大弹性势能为：Ep=mgssin37°+
mv02
代入数据解得：EP=38J．
（2）工件沿传送轨道减速向上滑动的过程中有：mgsin37°+μmgcos37°=ma1
代入数据解得a1=8m/s2．
从B点运动到与传送带共速需要的时间为： 
工件滑行的位移大小为： 
．
因为μ＜tan37°，所以工件将沿传送带继续减速上滑．有：
mgsin37°-μmgcos37°=ma2
代入数据解得：a2=4m/s2．
假设工件速度减为零时，工件未从传送带上滑落，则有： 
．
工件滑行的位移大小为：s2=
t2=2m=L-s1；
故假设成立，工件沿传送带上滑的时间为：t=t1+t2=1.5s．
（3）
练习册系列答案
相关题目
