��Ŀ����
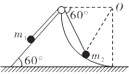
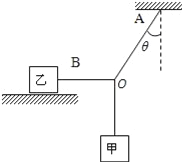
����Ŀ����ͼ��ʾ�����ʵ���һ�˹̶���ˮƽ����O���ת���ϣ���һ����һ����Ϊm�����ڴֲڹ̶�ֱ��A����С����Ϊ�ʵ㣩������ֱ�˵����Ϊ30�㣬OA=OC��BΪAC���е㣬OB���ڵ���ԭ����С���A���ɾ�ֹ��ʼ�»�����ʼ���ٶȴ�СΪaA �� ��һ�ξ���B�����ٶ�Ϊv���˶���C���ٶ�Ϊ0�������Դ�СΪaC�ij�ʼ���ٶ��ɾ�ֹ��ʼ���ϻ��У������Ħ�������ڻ���Ħ����������˵������ȷ���ǣ� ��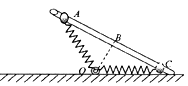
A.С����Է��ص�������A��
B.���ɾ��е����������Ϊ ![]() mv2
mv2
C.��ȥ���ɣ�С�������ֱ���ϴ��ھ�ֹ
D.aA��aC=g
���𰸡�B,D
���������⣺A��B����С���A�˶���B�Ĺ��̿˷�Ħ��������ΪWf��AB�����ֱ�߶�Ϊh��С�������Ϊm�����ɾ��е����������ΪEp��
���������غ㶨�ɣ�����С��A��B�Ĺ����У�mgh+Ep= ![]() +Wf��
+Wf��
A��C�Ĺ����У�2mgh+Ep=2Wf+Ep����ã�Wf=mgh��Ep= ![]() ��
��
С���C�������˶�ʱ�������ܷ��ص�A�㣬���������غ㶨�ɵã�
Ep=2Wf+2mgh+Ep����ʽΥ���������غ㶨�ɣ���֪С���ܷ��ص�������A������A����B��ȷ��
C�����A�˶���CĦ������ƽ��ֵΪ ![]() ��AB=s����Wf=mgh�ã�
��AB=s����Wf=mgh�ã�
![]() s=mgssin30��
s=mgssin30��
��B�㣬Ħ���� f=��mgcos30�㣬���ڵ��ɶ�С������������B���⣩��С��Ը˵�ѹ�����ڦ�mgcos30�㣬���� ![]() ����mgcos30��
����mgcos30��
�ɵ� mgsin30�㣾��mgcos30�㣬��˳�ȥ���ɣ�С������ֱ���ϴ��ھ�ֹ����C����
D������ţ�ٵڶ����ɵã�
��A���У�Fcos30��+mgsin30�㩁f=maA��
��C���У�Fcos30�㩁f��mgsin30��=maC��
��ʽ����ã�aA��aC=g����D��ȷ��
��ѡ��BD
����������б�����µķ��������Ħ�����Ĺ�ϵ���жϳ���ȥ���ɣ�С����ֱ���ϲ��ܴ��ھ�ֹ����С��A��B�Ĺ��̺�A��C�Ĺ��̣��ֱ���������غ㶨����ʽ������õ��ɾ��е���������ܣ���ţ�ٵڶ������о�A��C����ļ��ٶȣ���ȽϿɵõ�aA��aC=g��

 ������ÿ�ʱ�Ż���ҵϵ�д�
������ÿ�ʱ�Ż���ҵϵ�д�