题目内容
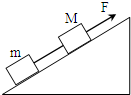 如图所示,斜面倾角为θ,其上由相同材料、质量分别为m和M的两物体用细绳连接,在M上施加沿斜面向上的恒力F,使两物体沿斜面做匀加速直线运动,在下列两种情况下求细绳的拉力:
如图所示,斜面倾角为θ,其上由相同材料、质量分别为m和M的两物体用细绳连接,在M上施加沿斜面向上的恒力F,使两物体沿斜面做匀加速直线运动,在下列两种情况下求细绳的拉力:(1)斜面光滑
(2)斜面和物体间的摩擦系数为μ.
分析:先整体受力分析,后隔离单独分析m,根据牛顿第二定律列式联立求解即可;
解答:解:(1)斜面光滑时,先由整体法分析,
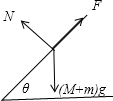
系统加速为a,根据牛顿第二定律可得:
F-(m+M)gsinθ=(M+m)a ①
隔离m,对m受力分析:
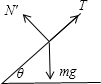
由牛顿第二定律可得:T-mgsinθ=ma ②
①②联立可得:T=
(2)斜面和物体间的摩擦系数为μ时,和上面不同的是有沿斜面向下的摩擦力.
对M和m整体分析,有:F-f-(M+m)gsinθ=(M+m)a
N=(M+m)gcosθ
f=μN
故:a=
-μgcosθ-gsinθ
对m受力分析,可得:T′-f′-mgsinθ=ma
N′=mgcosθ
f′=μN′
解得:T′=
答:(1)斜面光滑时,细绳的拉力为T=
;(2)斜面和物体间的摩擦系数为μ时,细绳的拉力为T′=
.

系统加速为a,根据牛顿第二定律可得:
F-(m+M)gsinθ=(M+m)a ①
隔离m,对m受力分析:

由牛顿第二定律可得:T-mgsinθ=ma ②
①②联立可得:T=
| Fm |
| M+m |
(2)斜面和物体间的摩擦系数为μ时,和上面不同的是有沿斜面向下的摩擦力.
对M和m整体分析,有:F-f-(M+m)gsinθ=(M+m)a
N=(M+m)gcosθ
f=μN
故:a=
| F |
| M+m |
对m受力分析,可得:T′-f′-mgsinθ=ma
N′=mgcosθ
f′=μN′
解得:T′=
| Fm |
| M+m |
答:(1)斜面光滑时,细绳的拉力为T=
| Fm |
| M+m |
| Fm |
| M+m |
点评:本题考查牛顿第二定律的实际应用,关键能够结合题目先整体再隔离分析法相结合,难度不大.

练习册系列答案
相关题目
 如图所示,斜面倾角为α,且sinα=0.6 cosα=0.8,当用228N的力拉绳时,人与板一起匀速上滑,当用132N的力拉绳时,人与板一起匀速下滑,若人重为500N,求
如图所示,斜面倾角为α,且sinα=0.6 cosα=0.8,当用228N的力拉绳时,人与板一起匀速上滑,当用132N的力拉绳时,人与板一起匀速下滑,若人重为500N,求 如图所示,斜面倾角为θ,木板A的质量为M,物块B的质量为m.绳的一端与B连接,另一端与固定在斜面上的挡板相连,绳与斜面平行.已知A与B间的动摩擦因数为μ1,A与斜面间的动摩擦因数为μ2.
如图所示,斜面倾角为θ,木板A的质量为M,物块B的质量为m.绳的一端与B连接,另一端与固定在斜面上的挡板相连,绳与斜面平行.已知A与B间的动摩擦因数为μ1,A与斜面间的动摩擦因数为μ2. 如图所示,斜面倾角为37°,静止滑下,物体与平面、斜面间的动摩擦因数均为0.3.求该物体下滑后将在距斜面底端多远处停止?(g=10m/s2)
如图所示,斜面倾角为37°,静止滑下,物体与平面、斜面间的动摩擦因数均为0.3.求该物体下滑后将在距斜面底端多远处停止?(g=10m/s2) 如图所示,斜面倾角为θ,从斜面上的A点以速度v0将一小球水平抛出,落在斜面的B点处,则小球从A点到B点的运动时间为
如图所示,斜面倾角为θ,从斜面上的A点以速度v0将一小球水平抛出,落在斜面的B点处,则小球从A点到B点的运动时间为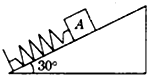 如图所示,斜面倾角为30°,物体A的重力为80N,物体与斜面间的最大静摩擦力为35N.一根原长为10cm,劲度系数为k=1000N/m的轻质弹簧,下端固定在斜面底端,上端与物体A固定连接放置好后,弹簧长度变为8cm.现要使物体移动,用平行于斜面的力作用在物体A上.则下面几个作用力中不可能的是( )
如图所示,斜面倾角为30°,物体A的重力为80N,物体与斜面间的最大静摩擦力为35N.一根原长为10cm,劲度系数为k=1000N/m的轻质弹簧,下端固定在斜面底端,上端与物体A固定连接放置好后,弹簧长度变为8cm.现要使物体移动,用平行于斜面的力作用在物体A上.则下面几个作用力中不可能的是( )