题目内容
如图所示，斜面倾角为θ，从斜面上的A点以速度v0将一小球水平抛出，落在斜面的B点处，则小球从A点到B点的运动时间为| 2v0tanθ |
| g |
| 2v0tanθ |
| g |
2v02sinθ/gcosθ2
2v02sinθ/gcosθ2
．分析：解决平抛运动的方法是把平抛运动分解到水平方向和竖直方向去研究，水平方向做匀速直线运动，竖直方向做自由落体运动，两个方向上运动的时间相同．
解答：解：设AB之间的距离为L，
则：水平方向：Lcosθ=V0t
竖直方向：Lsinθ=
gt2
联立解得：t=
所以L=
=
故答案为：
；
则：水平方向：Lcosθ=V0t
竖直方向：Lsinθ=
| 1 |
| 2 |
联立解得：t=
| 2v0tanθ |
| g |
所以L=
| v0t |
| cosθ |
| 2v02sinθ |
| g(cosθ)2 |
故答案为：
| 2v0tanθ |
| g |
| 2v02sinθ |
| g(cosθ)2 |
点评：本题就是对平抛运动规律的直接应用，本题难度不大．
练习册系列答案
相关题目
如图所示，斜面倾角为α，且sinα=0.6 cosα=0.8，当用228N的力拉绳时，人与板一起匀速上滑，当用132N的力拉绳时，人与板一起匀速下滑，若人重为500N，求
如图所示，斜面倾角为θ，木板A的质量为M，物块B的质量为m．绳的一端与B连接，另一端与固定在斜面上的挡板相连，绳与斜面平行．已知A与B间的动摩擦因数为μ1，A与斜面间的动摩擦因数为μ2．
如图所示，斜面倾角为37°，静止滑下，物体与平面、斜面间的动摩擦因数均为0.3．求该物体下滑后将在距斜面底端多远处停止？（g=10m/s2）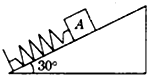
如图所示，斜面倾角为30°，物体A的重力为80N，物体与斜面间的最大静摩擦力为35N．一根原长为10cm，劲度系数为k=1000N/m的轻质弹簧，下端固定在斜面底端，上端与物体A固定连接放置好后，弹簧长度变为8cm．现要使物体移动，用平行于斜面的力作用在物体A上．则下面几个作用力中不可能的是（ ）