题目内容
17.如图所示,在水平放置的足够大荧光屏PQMN上方存在着磁感应强度大小为B的匀强磁场,方向平行于水平面且与边MQ垂直.某时刻从与该平面相距为h的S点(S在平面上的投影位置为A)向垂直磁场的平面内的各个方向同时发射大量相同带正电的粒子,粒子质量均为m,电量为q,速度大小均为v=$\frac{5Bqh}{8m}$,方向均在同一竖直平面内.观察发现,荧光屏上OF之间有发光,其余位置均无发光,且OF间某些位置只有一次发光,某些位置有两次放光,试求:
(1)发光区域OF的长度;
(2)荧光屏上一次发光的区域长度与两次发光的区域长度之比.
分析 (1)由洛伦兹力通过向心力得出粒子运动的半径,然后通过作图,寻找出半径与各点之间的几何关系,即可求出发光区域OF的长度;
(2)分析发光点的移动的特点,然后即可确定.
解答 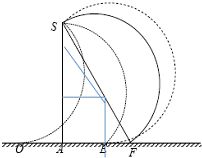 解:(1)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,得:$qvB=\frac{m{v}^{2}}{r}$
解:(1)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,得:$qvB=\frac{m{v}^{2}}{r}$
所以粒子的运动半径:$r=\frac{mv}{qB}$=$\frac{5}{8}h$
所以离子源到离A点最远的F之间的距离:$SF=2r=\frac{5h}{4}$
则:$AF=\frac{3}{4}h$
设AE=x,则有:$\sqrt{{r}^{2}+{x}^{2}}+r=h$
得:$x=\frac{1}{2}h$
显然:AO=AE
故:$OF=\frac{1}{2}h+\frac{3}{4}h=\frac{5}{4}h$
(2)荧光屏上最先发光的位置在O点,逐渐向右移动,直到F点后再返回发光,回到E点后发光消失,所以一次发光的区域为OE,两次发光区域为EF.
$\frac{OE}{EF}=\frac{\frac{1}{2}h+\frac{1}{2}h}{\frac{3}{4}h+\frac{1}{2}h}=\frac{4}{1}$
答:(1)发光区域OF的长度是$\frac{5}{4}h$;
(2)荧光屏上一次发光的区域长度与两次发光的区域长度之比是4:1.
点评 带电粒子在磁场中的运动要明确粒子运动的运动性质,结合几何知识,根据运动性质寻找合适的解题方法.

练习册系列答案
相关题目
7.“太空涂鸦”技术的基本物理模型是:原来在较低圆轨道运行的攻击卫星在从后方接近在较高圆轨道上运行的侦察卫星时,准确计算轨道并向其发射“漆雾”弹,“漆雾”弹在临近侦察卫星时,压爆弹囊,让“漆雾”散开并喷向侦察卫星,喷散后强力吸附在侦察卫星的侦察镜头、太阳能板、电子侦察传感器等关键设备上,使之暂时失效.下列说法正确的是( )
| A. | 攻击卫星在原轨道上运行的线速度大于7.9 km/s | |
| B. | 攻击卫星在原轨道上运行的线速度比侦察卫星的线速度小 | |
| C. | 攻击卫星完成“太空涂鸦”后应减速才能返回低轨道上 | |
| D. | 若攻击卫星周期已知,结合万有引力常量就可计算出地球质量 |
5.关于电磁波和相对论,下列说法正确的是( )
| A. | 由于高频电磁波向外界辐射能量的本领更强,所以经过调制的高频电磁波才能把我们要发射的信号发射出去 | |
| B. | 电磁波是由恒定的电场和磁场产生的 | |
| C. | 研究高速火车的运动必须利用相对沦的知识 | |
| D. | 研究速度接近于光速的粒子的运动利用相对论的知识 |
2.某时刻,质量为2kg的物体甲受到的合力是6N,速度是10m/s;质量为3kg的物体乙受到的合力是5N,速度是10m/s,则( )
| A. | 甲比乙的惯性小 | B. | 甲比乙的惯性大 | ||
| C. | 甲和乙的惯性一大 | D. | 无法判定哪个物体惯性大 |
9.下列说法中不正确的是( )
| A. | 电动机是把其他形式的能转化为电能的装置 | |
| B. | 发电机是把其他形式的能转化为电能的装置 | |
| C. | 电容器是储存电荷的装置 | |
| D. | 白炽灯是利用电流的热效应工作的 |
6.崔牛先生向客户推介他设计的“超级推进器”,该推进器由超导体、激光器、致冷剂以及计算机控制系统组成,其神奇之处在于能通过自身的循环工作,源源不断地获得动力,而不需要消耗任何能源.事实上,这是不可能实现的,因为他的设计违反了( )
| A. | 能量守恒定律 | B. | 电荷守恒定律 | C. | 机械能守恒定律 | D. | 质量守恒定律 |

 如图所示,M,N两极板间存在匀强电场,两极板的宽度为d,N板右边存在如图所示的磁场,折线PAQ是磁场的分界线,在折线的两侧分布着方向相反、与平面垂直的匀强磁场,磁感应强度大小都为B.折线的顶角∠A=90°,P、Q是折线上的两点,AP=AQ=L.现有一质量为m、电荷量为q的带负电微粒从S由静止经电场加速后再从P点沿PQ方向水平射出,不计微粒的重力.
如图所示,M,N两极板间存在匀强电场,两极板的宽度为d,N板右边存在如图所示的磁场,折线PAQ是磁场的分界线,在折线的两侧分布着方向相反、与平面垂直的匀强磁场,磁感应强度大小都为B.折线的顶角∠A=90°,P、Q是折线上的两点,AP=AQ=L.现有一质量为m、电荷量为q的带负电微粒从S由静止经电场加速后再从P点沿PQ方向水平射出,不计微粒的重力.