题目内容
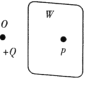
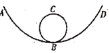
【题目】如图所示，一个小球（视为质点）从H=18m高处，由静止开始通过光滑弧形轨道AB，进入半径R=6m的竖直圆环，且与圆环间动摩擦因数处处相等，当到达环顶C时，刚好对轨道压力为零；沿CB圆弧滑下后，进入光滑弧形轨道BD，且到达高度为h的D点时的速度为零，g=10m/s2，所有高度均相对B点而言，则h值可能为（ ）
A. 10m B. 11m C. 12m D. 13m
【答案】D
【解析】
小球到达环顶C时，刚好对轨道压力为零，所以在C点，重力充当向心力，由牛顿第二定律得：
.已知圆环半径R=6m，小球在C点动能：
，以B所在平面为零势能面，在C点，小球重力势能EP=2mgR=12mg，小球从静止开始运动到到达C点过程中由动能定理得：
，解得Wf=-3mg，小球在C点时的机械能：E=EK+EP=15mg.由于克服摩擦力做功，机械能减少，小球到达底端时的机械能小于15mg；
小球从C点下滑过程中克服摩擦力做功，机械能减少，到达轨道同一高度处的速度比上升时的速度小，小球对轨道压力变小，摩擦力变小，小球下滑时，克服摩擦力做功小于3mg，故小球到达底端时的机械能大于15mg-3mg=12mg，小球进入光滑弧形轨道BD时，小球机械能的范围为，12mg＜E＜15mg，小球到达最高点时的机械能E=mgh，则12m＜h＜15m，故A，B，C错误，D正确.故选D.
练习册系列答案
相关题目
