题目内容
【题目】如图所示，一很长的、不可伸长的柔软轻绳跨过光滑定滑轮，绳两端各系一小球a和b．a球质量为m，静置于地面：b球质量为3m，用手托住，高度为h，此时轻绳刚好拉紧．
求从静止开始释放b后，a能离地面的最大高度．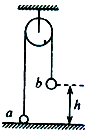
【答案】解：设a球到达高度h时两球的速度v，根据系统的机械能守恒得：
3mgh=mgh+ 
（3m+m）v2
解得 两球的速度都为 v= 
此时绳子恰好放松，a球开始做初速度为 v= 的竖直上抛运动，
设物体b能上升的最大高度为H．
对a，根据机械能守恒：mgh+ 
=mgH
解得a球能达到的最大高度H为1.5h．
答：从静止开始释放b后，a能离地面的最大高度是1.5h．
【解析】本题可以分为两个过程来求解，首先根据ab系统的机械能守恒，可以求得a球上升h时的速度的大小，之后，b球落地，a球的机械能守恒，从而可以求得a球上升的高度的大小．
【考点精析】解答此题的关键在于理解机械能综合应用的相关知识，掌握系统初态的总机械能E 1 等于末态的总机械能E 2 ，即E1 =E2；系统减少的总重力势能ΔE P减 等于系统增加的总动能ΔE K增 ，即ΔE P减 =ΔE K增；若系统只有A、
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
