题目内容
12.在抗震救灾中常常利用悬停直升机向灾区空投救灾物资(如图甲).对于医药救灾物资只能从不高于h=20m处自由释放才能安全着地,实际一些灾区往往地处深山峡谷,直升机能够安全悬停的高度比h要高得多,直接空投会造成损失.为解决这一问题,“我爱发明”研究小组设计了一台限速装置,不论从多高处释放物资,最终都能以安全速度着地.该装置简化工作原理如图乙所示,竖直绝缘圆盘可以绕圆心O自由转动,其上固定半径分别为r1=1m和r2=0.5m的两个同心金属圆环,连接两圆环的金属杆EF的延长线通过圆心O,足够长的不可伸长的轻质细绳一端缠绕在大金属圆环上,另一端通过光滑滑轮挂救灾物资,圆环上的a点和b点通过电刷连接一可调电阻R,两圆环之间区域存在垂直于圆盘平面向内的匀强磁场,磁感应强度B=40T.(细绳与大金属圆环间没有滑动,金属杆、金属圆环、导线及电刷的电阻均不计,空气阻力及一切摩擦均不计,重力加速度g=10m/s2)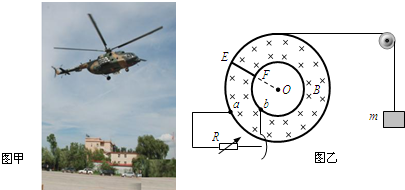
(1)求医药物资能安全着地的最大速度;
(2)利用该装置使医药物资以最大安全速度匀速下降,求此时电阻R两端的电势差;
(3)若医药物资的质量m=60kg,应如何设置可调电阻R的阻值?
(4)试推导质量为m的医药物资在匀速下降时,金属杆EF所受安培力与重力的大小关系.
分析 (1)根据自由落体运动位移与速度公式,即可求解;
(2)根据法拉第电磁感应定律,结合几何关系求得面积,从而求得电阻R两端的电势差;
(3)由能量守恒关系,重力的功率等于发热功率,从而求得可调电阻的阻值范围;
(4)根据安培力表达式F=BIL,结合mgv=$\frac{{E}^{2}}{R}$,和E=$\frac{1}{2}B(v+\frac{v}{2})({r}_{1}-{r}_{2})$,即可求解.
解答 解:(1)设医药物资安全到达地面的最大速度为v,
根据自由落体运动可知,则有:v=$\sqrt{2gh}$,解得:v=$\sqrt{2×10×20}$=20m/s;
(2)在△t时间内,金属杆EF扫过的面积为:△S=$\frac{1}{2}(v△t+\frac{v}{2}△t)({r}_{1}-{r}_{2})$
由法拉第电磁感应定律,金属杆上感应电动势的大小为E=$\frac{△∅}{△t}$=$\frac{B△S}{△t}$=$\frac{1}{2}B(v+\frac{v}{2})({r}_{1}-{r}_{2})$;
解得:E=300V,
则电阻R两端的电势差为300V;
(3)医药物资以最大安全速度下降时,由能量关系可知,mgv=$\frac{{E}^{2}}{R}$
解得:R=7.5Ω
可调电阻R的阻值应大于或等于7.5Ω;
(4)设金属杆EF所受安培力为F,则有:F=BIL=B$\frac{E}{R}$(r1-r2)
将mgv=$\frac{{E}^{2}}{R}$,和E=$\frac{1}{2}B(v+\frac{v}{2})({r}_{1}-{r}_{2})$代入;
解得:F=$\frac{4}{3}mg$
答:(1)医药物资能安全着地的最大速度20m/s;
(2)利用该装置使医药物资以最大安全速度匀速下降,此时电阻R两端的电势差300V;
(3)若医药物资的质量m=60kg,应可调电阻R的阻值应大于或等于7.5Ω;
(4)质量为m的医药物资在匀速下降时,金属杆EF所受安培力与重力的大小关系F=$\frac{4}{3}mg$.
点评 考查运动学公式、法拉第电磁感应定律的内容,掌握能量守恒关系,知道安培力表达式应用,并注意扫过面积求法.

 阅读快车系列答案
阅读快车系列答案| A. | 千克•米/秒 | B. | 焦/米 | ||
| C. | 库仑•米/秒•特斯拉 | D. | 特斯拉•安培•米2 |
 如图所示,A、B、C为放置在光滑水平面上的三个带电小球,其中B与C之间用长为L的绝缘轻质细杆相连(L远远大于小球的直径),现在三个小球都恰好处于静止状态.已知小球B的带电量为-q,小球C的带电量为+9q,则以下判断正确的是( )
如图所示,A、B、C为放置在光滑水平面上的三个带电小球,其中B与C之间用长为L的绝缘轻质细杆相连(L远远大于小球的直径),现在三个小球都恰好处于静止状态.已知小球B的带电量为-q,小球C的带电量为+9q,则以下判断正确的是( )| A. | 小球A的带电量一定为+$\frac{9q}{4}$ | |
| B. | 轻质细杆一定处于被拉伸状态 | |
| C. | 小球A与B之间的距离一定为$\frac{L}{2}$ | |
| D. | 若将A向右平移一小段距离,释放后A一定向左运动 |
 如图所示,有一定质量的理想气体密闭在导热性能良好的气缸内,现通过外力使活塞缓慢向左移动一小段距离,设外部环境温度不变,则( )
如图所示,有一定质量的理想气体密闭在导热性能良好的气缸内,现通过外力使活塞缓慢向左移动一小段距离,设外部环境温度不变,则( )| A. | 气体温度上升 | B. | 气体压强增大 | ||
| C. | 气体分子间的引力和斥力均增大 | D. | 气体对外放出热量 |
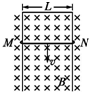 如图所示,竖直平面内有一宽度为0.5m且足够长的“U”形金属导轨,处在磁感应强度大小为0.2T、方向与导轨平面垂直的匀强磁场中,导体棒MN沿导轨以1.0m/s的速度竖直向下匀速运动了2.0s.求:
如图所示,竖直平面内有一宽度为0.5m且足够长的“U”形金属导轨,处在磁感应强度大小为0.2T、方向与导轨平面垂直的匀强磁场中,导体棒MN沿导轨以1.0m/s的速度竖直向下匀速运动了2.0s.求: 如图所示,是一研究带电粒子运动的装置图,区域I中有垂直纸面向外的磁感应强度为B1的匀强磁场和竖起方向的匀强电场.平行板间距为2R,且足够长.区域II中有圆心坐标为(0,R),半径为R的圆形磁场,磁感应强度B2=$\frac{mυ}{qR}$方向垂直纸面向外,质量为m,电荷量为+q的速度不同的粒子从左侧射入区域I,经区域I后,只有沿x轴正向的速率为υ,分布宽度为2R的粒子射出,出射后的粒子进入区域Ⅱ,不计粒子重力.
如图所示,是一研究带电粒子运动的装置图,区域I中有垂直纸面向外的磁感应强度为B1的匀强磁场和竖起方向的匀强电场.平行板间距为2R,且足够长.区域II中有圆心坐标为(0,R),半径为R的圆形磁场,磁感应强度B2=$\frac{mυ}{qR}$方向垂直纸面向外,质量为m,电荷量为+q的速度不同的粒子从左侧射入区域I,经区域I后,只有沿x轴正向的速率为υ,分布宽度为2R的粒子射出,出射后的粒子进入区域Ⅱ,不计粒子重力.

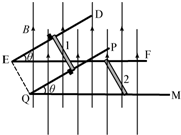 如图所示,空间中有竖直向上的匀强磁场,磁感应强度B=0.5T.DEF和PQM为两条相同的折线金属导轨(电阻不计),其中EF和QM构成导轨的水平部分,ED和QP构成导轨的倾斜部分,倾角θ=37°.导轨的水平部分和倾斜部分均足够长且光滑,导轨的间距L=1m.导轨的倾斜部分有两个固定的小挡片,在小挡片上放有质量m1=0.2kg,电阻R1=1Ω,长度为L的导体棒1,导体棒与导轨垂直;在导轨的水平部分垂直导轨放置一个质量m2=0.2kg,电阻R2=1Ω、长度为L的导体棒2.开始时,两导体棒均静止,现在对导体棒2施加一个水平向右的外力,使导体棒2从静止开始做加速度a=2m/s2的匀加速直线运动.
如图所示,空间中有竖直向上的匀强磁场,磁感应强度B=0.5T.DEF和PQM为两条相同的折线金属导轨(电阻不计),其中EF和QM构成导轨的水平部分,ED和QP构成导轨的倾斜部分,倾角θ=37°.导轨的水平部分和倾斜部分均足够长且光滑,导轨的间距L=1m.导轨的倾斜部分有两个固定的小挡片,在小挡片上放有质量m1=0.2kg,电阻R1=1Ω,长度为L的导体棒1,导体棒与导轨垂直;在导轨的水平部分垂直导轨放置一个质量m2=0.2kg,电阻R2=1Ω、长度为L的导体棒2.开始时,两导体棒均静止,现在对导体棒2施加一个水平向右的外力,使导体棒2从静止开始做加速度a=2m/s2的匀加速直线运动.