题目内容
12.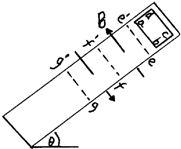 如图所示,在倾角为θ的光滑绝缘斜面上,存在着两个磁感应强度相等的匀强磁场,方向一个垂直斜面向上,另一个垂直斜面向下,宽度均为l,一个质量为m,边长也为l的正方形线框以速度v进入上边磁场时,恰好做匀速运动,求:
如图所示,在倾角为θ的光滑绝缘斜面上,存在着两个磁感应强度相等的匀强磁场,方向一个垂直斜面向上,另一个垂直斜面向下,宽度均为l,一个质量为m,边长也为l的正方形线框以速度v进入上边磁场时,恰好做匀速运动,求:(1)当ab边刚越过ff′时,线框的加速度多大?方向如何?
(2)当ab边到达gg′与ff′正中间位置时,线框又恰好做匀速运动,问线框从开始进入上边磁场到ab边到达gg′与ff′正中间位置过程中,放出的热量是多少?
分析 (1)线框开始进入磁场时做匀速直线运动,由平衡条件可以求出线框速度,当ab边刚越过ff′时,由牛顿第二定律可以求出线框的加速度.
(2)由能量守恒定律可以求出线框产生的热量.
解答 解:(1)线框进入磁场时受到的安培力:F=BIL=B2L2vRB2L2vR,
ab边刚越过ee′即做匀速直线运动,由平衡条件得:mgsinθ=B2L2vRB2L2vR,
在ab边刚越过ff′时,ab、cd 边都切割磁感线产生感应电动势,但线框的运动速度不能突变,则此时回路中的总感应电动势为:E=2BLv.
此时线框受到的安培力为:F′=2BI′L=4B2L2vR4B2L2vR,
由牛顿第二定律得:4B2L2vR4B2L2vR-mgsinθ=ma,
解得:a=3gsinθ,方向沿斜面向上.
(2)设线框再做匀速运动的速度为v′,由平衡条件得:mgsinθ=2×2B2L2v′R,
解得:v′=v4,
线框从过ee′到再做匀速运动过程中,设产生的热量为Q,由能量守恒定律得:
Q=mg•32Lsinθ+12mv2−12mv′2=3mgLsinθ2+1532mv2;
答:(1)当ab边刚越过ff′时,线框加速度的值为3gsinθ.
(2)求线框从开始进入磁场到ab边到达gg′和ff′中点的过程中产生的热量是3mgLsinθ2+1532mv2.
点评 本题的易错点在于ab、cd两边均在磁场中时,两个边都切割磁感线,注意此时回路中的电动势为E=2BLv.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
15.行驶中汽车制动后滑行一段距离,最后停下;流星在夜空中坠落并发出明亮的光焰;降落伞在空中匀速下降.上述不同现象所包含的相同的物理过程是( )
①物体克服阻力做功
②物体的动能转化为其他形式的能量
③物体的势能转化为其他形式的能量
④物体的机械能转化为其他形式的能量.
①物体克服阻力做功
②物体的动能转化为其他形式的能量
③物体的势能转化为其他形式的能量
④物体的机械能转化为其他形式的能量.
| A. | ② | B. | ①② | C. | ①③ | D. | ①④ |
16.电阻R1,R2分别接在完全相同的电源上,已知电源的内阻为3Ω,当R1,R2的阻值满足下列哪些关系时,两个电阻上消耗的电功率相同( )
| A. | R1=R2=3Ω | B. | R1=1Ω,R2=9Ω | C. | R1=2Ω,R2=4.5Ω | D. | R1=3Ω,R2=4Ω |
13. 如图所示,放在倾角为θ的斜面上的质量为m的木块静止不动,将木块所受的重力分解为垂直于斜面的分力F1和平行于斜面向下的分力F2,下列说法正确的是( )
如图所示,放在倾角为θ的斜面上的质量为m的木块静止不动,将木块所受的重力分解为垂直于斜面的分力F1和平行于斜面向下的分力F2,下列说法正确的是( )
 如图所示,放在倾角为θ的斜面上的质量为m的木块静止不动,将木块所受的重力分解为垂直于斜面的分力F1和平行于斜面向下的分力F2,下列说法正确的是( )
如图所示,放在倾角为θ的斜面上的质量为m的木块静止不动,将木块所受的重力分解为垂直于斜面的分力F1和平行于斜面向下的分力F2,下列说法正确的是( )| A. | 分力F1和F2的大小为F1=mgsinθ,F2=mgcosθ | |
| B. | 分力F1和F2的大小为F1=mgcosθ,F2=mgsinθ | |
| C. | F1是木块对斜面的压力 | |
| D. | 木块所受斜面的摩擦力大小为mgsinθ |
7. 关于回旋加速器,下列说法中正确的是( )
关于回旋加速器,下列说法中正确的是( )
 关于回旋加速器,下列说法中正确的是( )
关于回旋加速器,下列说法中正确的是( )| A. | 在B一定的情况,D形盒的半径越大,同一带电粒子获得的动能越大 | |
| B. | 在回旋加速器D形盒的半径一定的情况下,磁场越强,同一带电粒子获的动能越大 | |
| C. | 在回旋加速器半径一定的情况下,同一带电粒子获得的动能与交流电源的电压无关 | |
| D. | 在磁感应强度和回旋加速器半径一定的情况下,交流电源的电压越大,同一带电粒子获得的动能越大 |
 是量程为2A的标准电流表,R0为电阻箱,R为滑动变阻器,S为开关,E为电源.
是量程为2A的标准电流表,R0为电阻箱,R为滑动变阻器,S为开关,E为电源.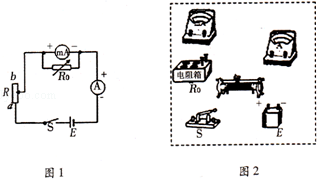
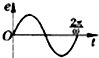
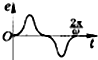
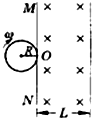 如图所示,直线MN右边区域宽度为L的空间,存在磁感强度为B的匀强磁场,磁场方向垂直纸面向里.由导线弯成的半径为R(L>2R)的圆环处在垂直于磁场的平面内,且可绕环与MN的切点O在该平面内转动.现让环以角速度ω顺时针匀速转动.如图环从图示位置开始转过一周的过程中,感应电动势的瞬时值随时间变化的图象,正确的是( )
如图所示,直线MN右边区域宽度为L的空间,存在磁感强度为B的匀强磁场,磁场方向垂直纸面向里.由导线弯成的半径为R(L>2R)的圆环处在垂直于磁场的平面内,且可绕环与MN的切点O在该平面内转动.现让环以角速度ω顺时针匀速转动.如图环从图示位置开始转过一周的过程中,感应电动势的瞬时值随时间变化的图象,正确的是( )