题目内容
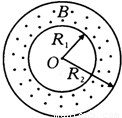
在受控热核聚变反应的装置中温度极高,因而带电粒子没有通常意义上的容器可装,而是由磁场将带电粒子的运动束缚在某个区域内.现有一个环形区域,其截面内圆半径R1=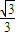 m,外圆半径R2=1.0m,区域内有垂直纸面向外的匀强磁场(如图所示).已知磁感应强度B=1.0T,被束缚带正电粒子的荷质比为
m,外圆半径R2=1.0m,区域内有垂直纸面向外的匀强磁场(如图所示).已知磁感应强度B=1.0T,被束缚带正电粒子的荷质比为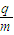 =4.0×107C/kg,不计带电粒子的重力和它们之间的相互作用.
=4.0×107C/kg,不计带电粒子的重力和它们之间的相互作用.(1)若中空区域中的带电粒子由O点沿环的半径方向射入磁场,求带电粒子不能穿越磁场外边界的最
大速度vo.
(2)若中空区域中的带电粒子以(1)中的最大速度vo沿圆环半径方向射入磁场,求带电粒子从刚进入磁
场某点开始到第一次回到该点所需要的时间t.

【答案】分析:(1)根据几何关系与牛顿第二定律,即可求解;
(2)根据几何关系,可确定θ的值,并由周期公式与圆心角,可求出在磁场中运动的时间,再由运动学公式,可求出在磁场外运动的时间,最后可确定总时间.
解答: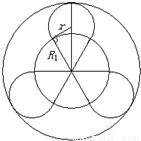 解:(1)根据几何关系,则有:
解:(1)根据几何关系,则有: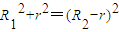
解得: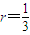
由牛顿第二定律,则有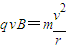
解得: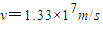
(2)如图,则有: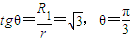 ,
,
带电粒子必须三次经过磁场,才会回到该点
在磁场中的圆心角为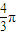 ,则在磁场中运动的时间为
,则在磁场中运动的时间为
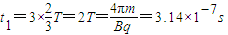
在磁场外运动的时间为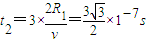
则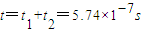
答:(1)若中空区域中的带电粒子由O点沿环的半径方向射入磁场,求带电粒子不能穿越磁场外边界的最大速度: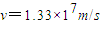 .
.
(2)若中空区域中的带电粒子以(1)中的最大速度vo沿圆环半径方向射入磁场,则带电粒子从刚进入磁场某点开始到第一次回到该点所需要的时间5.74×10-7s.
点评:考查牛顿第二定律与运动学公式,掌握如何画出运动轨迹图,学会求在磁场中运动的时间.
(2)根据几何关系,可确定θ的值,并由周期公式与圆心角,可求出在磁场中运动的时间,再由运动学公式,可求出在磁场外运动的时间,最后可确定总时间.
解答:
 解:(1)根据几何关系,则有:
解:(1)根据几何关系,则有: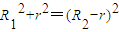
解得:
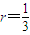
由牛顿第二定律,则有
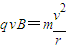
解得:
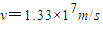
(2)如图,则有:
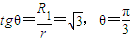 ,
,带电粒子必须三次经过磁场,才会回到该点
在磁场中的圆心角为
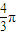 ,则在磁场中运动的时间为
,则在磁场中运动的时间为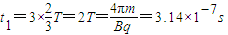
在磁场外运动的时间为
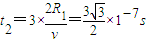
则
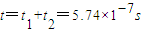
答:(1)若中空区域中的带电粒子由O点沿环的半径方向射入磁场,求带电粒子不能穿越磁场外边界的最大速度:
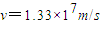 .
.(2)若中空区域中的带电粒子以(1)中的最大速度vo沿圆环半径方向射入磁场,则带电粒子从刚进入磁场某点开始到第一次回到该点所需要的时间5.74×10-7s.
点评:考查牛顿第二定律与运动学公式,掌握如何画出运动轨迹图,学会求在磁场中运动的时间.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 在受控热核聚变反应的装置中温度极高,因而带电粒子没有通常意义上的容器可装,而是由磁场将带电粒子的运动束缚在某个区域内.现有一个环形区域,其截面内圆半径R1=
在受控热核聚变反应的装置中温度极高,因而带电粒子没有通常意义上的容器可装,而是由磁场将带电粒子的运动束缚在某个区域内.现有一个环形区域,其截面内圆半径R1=
 m,外圆半径R2=1.0m,区域内有垂直纸面向外的匀强磁场(如图所示).已知磁感应强度B=1.0T,被束缚带正电粒子的荷质比为
m,外圆半径R2=1.0m,区域内有垂直纸面向外的匀强磁场(如图所示).已知磁感应强度B=1.0T,被束缚带正电粒子的荷质比为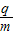 =4.0×107C/kg,不计带电粒子的重力和它们之间的相互作用.
=4.0×107C/kg,不计带电粒子的重力和它们之间的相互作用.