题目内容
在图示的装置中，表面粗糙的斜面固定在地面上，斜面的倾角θ=30°．两个光滑的定滑轮的半径很小，用一根跨过定滑轮的细线连接甲、乙两物体，把甲物体放在斜面上且连线与斜面平行，把乙物体拉开使悬线拉直且偏离竖直方向α=60°．现同时由静止释放甲、乙两物体，乙物体将在竖直平面内摆动，当乙物体运动经过最高点和最低点时，甲物体在斜面上所受摩擦力均为最大但未滑动．已知乙物体的质量m=1kg，取g=10m/s2，下列判断正确的是（ ）分析：乙物体摆到最高点时绳子拉力最小，根据沿绳子方向合力为零求出绳子的拉力；摆到最低点时绳子拉力最大，根据动能定理结合牛顿第二定律求出乙物体在最低点时绳子的拉力．当绳子的拉力最小时，甲物体有沿斜面向上的最大静摩擦力，当绳子拉力最大时，甲物体有沿斜面向下的最大静摩擦力，根据共点力平衡求出甲物体的质量和斜面对甲物体的最大静摩擦力．
解答：解：A、乙物体摆到最高点时绳子拉力最小，有：m乙gcos60°=T1=5N．故A正确．
B、由最高点到最低点，根据动能定理得：mgl（1-cos60°）=
mv2
根据牛顿第二定律得：T2-mg=m
联立两式得：T2=20N．故B错误．
C、D对甲物体有：m甲gsin30°=T1+fm，m甲gsin30°+fm=T2，联立两式得，甲的质量为：m甲=2.5kg，甲所受的最大静摩擦力为：fm=7.5N．故C错误，D正确．
故选：AD．
B、由最高点到最低点，根据动能定理得：mgl（1-cos60°）=
| 1 |
| 2 |
根据牛顿第二定律得：T2-mg=m
| v2 |
| l |
联立两式得：T2=20N．故B错误．
C、D对甲物体有：m甲gsin30°=T1+fm，m甲gsin30°+fm=T2，联立两式得，甲的质量为：m甲=2.5kg，甲所受的最大静摩擦力为：fm=7.5N．故C错误，D正确．
故选：AD．
点评：解决本题的关键知道乙物体摆到最低点时有最大拉力，摆到最高点时有最小拉力．以及知道在乙物体摆到最低点时有沿斜面向下的最大静摩擦力，摆到最高点时有沿斜面向上的最大静摩擦力．
练习册系列答案
相关题目
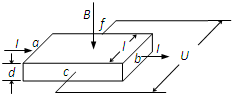用如图所示的装置可以测定导体中单位体积内的自由电子数n．现测得一块横截面为矩形的金属导体的宽度为l，厚为d，与侧面垂直的匀强磁场磁感应强度为B．当通以图示方向电流I时，在导体c、f表面间用电压表可测得电压U．已知自由电子的电荷量为e，则下列判断正确的是（ ）| A、c表面电势高 | ||
| B、f表面电势高 | ||
C、该导体单位体积内的自由电子数为
| ||
D、该导体单位体积内的自由电子数为
|
250mA，内阻约5Ω）；
250mA，内阻约5Ω）；
