题目内容
15．一个空气平行板电容器，极板间距离为d，正对面积为s，充以电荷量Q后，极板间电压为U，为使电容器的电容加倍，可采用的办法是（ ）| A． | 将电压变为一半 | |
| B． | 将所带电荷量变为2Q | |
| C． | 将极板正对面积变为2S | |
| D． | 将两极板间充满相对介电常数为2的电介质 |
分析 改变电容器的电压和带电量不会改变电容器的电容，由电容器的决定式$C=\frac{{ε}_{r}s}{4πkd}$得：我们可以通过改变正对面积s，介电常数eγ，极板间的距离d来改变电容．
解答 解：A、改变电容器的电压和带电量不会改变电容器的电容，由电容器的决定式$C=\frac{{ε}_{r}s}{4πkd}$决定的．故AB错误．
B、由电容器的决定式$C=\frac{{ε}_{r}s}{4πkd}$得：将电容器的电容加倍，我们可采取的方式是：①将极板正对面积变为2S；②将电解质换为介电常数为原来的介电常数2倍的电解质；③将两极板距离变为原来的一半．故CD正确；
故选：CD
点评 本题考查电容器的决定式，要明确改变电容器的电压和带电量不会改变电容器的电容，电容器的电容是由决定式$C=\frac{{ε}_{r}s}{4πkd}$决定的．
练习册系列答案
相关题目
5．如图所示为一质点运动的速度-时间图象，曲线为一正弦曲线的上半部，则在0～t1这段时间内（ ）
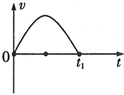
| A． | 质点的速度先减小后增大 | |
| B． | 质点在t1时刻离开出发点最远 | |
| C． | 质点运动的加速度先减小后增大 | |
| D． | 图中正弦曲线是质点的实际运动轨迹 |
6．物体静止在离水平地面一定高出时具有60J的重力势能（以水平地面为重力势能零参考平面），自由下落至某一位置时其重力势能为动能的一半．那么，该过程物体重力势能的减少量是（ ）
| A． | 20J | B． | 30J | C． | 40J | D． | 60J |
3．
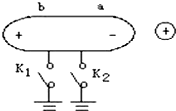如图所示，把一个不带电的枕型导体靠近带正电的小球，由于静电感应，在左端a，右端b分别出现负、正电荷，则以下说法正确的是（ ）
如图所示，把一个不带电的枕型导体靠近带正电的小球，由于静电感应，在左端a，右端b分别出现负、正电荷，则以下说法正确的是（ ）| A． | 闭合K1，有电子从枕型导体流向大地 | |
| B． | 闭合K1，有正电荷从枕型导体流向大地 | |
| C． | 闭合K2，有电子从大地流向枕型导体 | |
| D． | 闭合K2，有电子从枕形导体流向大地 |
10．
一端装有定滑轮的粗糙斜面体放在地面上，A、B两物体通过细绳连接，并处于静止状态（不计绳的质量和绳与滑轮间的摩擦），如图所示．现用水平力F作用于物体B上，缓慢拉开一小角度此过程中斜面体与物体A仍然静止．则下列说法正确的是（ ）
一端装有定滑轮的粗糙斜面体放在地面上，A、B两物体通过细绳连接，并处于静止状态（不计绳的质量和绳与滑轮间的摩擦），如图所示．现用水平力F作用于物体B上，缓慢拉开一小角度此过程中斜面体与物体A仍然静止．则下列说法正确的是（ ）| A． | 缓慢拉开B的过程，水平力F不变 | |
| B． | 物体A所受斜面体的摩擦力一定变大 | |
| C． | 斜面对物体A作用力合力不变 | |
| D． | 斜面体所受地面的支持力一定不变 |
7．
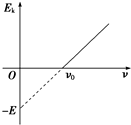如图所示是某金属在光的照射下产生的光电子的最大初动能Ek与入射光频率ν的关系图象．由图象可知（ ）
如图所示是某金属在光的照射下产生的光电子的最大初动能Ek与入射光频率ν的关系图象．由图象可知（ ）| A． | 该金属的逸出功等于E | |
| B． | 该金属的逸出功等于hν0 | |
| C． | 入射光的频率为3ν0时，产生的光电子的最大初动能为2E | |
| D． | 入射光的频率为$\frac{{v}_{0}}{2}$时，产生的光电子的最大初动能为$\frac{E}{2}$ |
9．某实验小组利用如图a所示的实验装置来探究当小车质量M一定时，物体运动的加速度a与其所受外力F之间的关系．
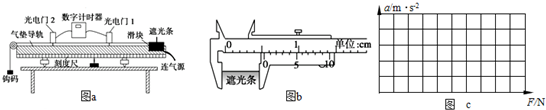
（1）由图中刻度尺读出两个光电门中心之间的距离x=24cm，由图b中游标卡尺测得遮光条的宽度d=0.52 cm．该实验小组在做实验时，将滑块从如图a所示位置由静止释放，由数字计时器可以读出遮光条通过光电门1的时间△t1，遮光条通过光电门2的时间△t2，则滑块经过光电门1时的瞬时速度的表达式v1=$\frac{d}{△{t}_{1}}$，滑块经过光电门2时的瞬时速度的表达式v2=$\frac{d}{△{t}_{2}}$，则滑块的加速度的表达式a=$\frac{{（\frac{d}{△{t}_{2}}）}^{2}-{（\frac{d}{△{t}_{1}}）}^{2}}{2x}$．（用字母表示）
（2）在本次实验中，实验小组通过改变钩码质量m总共做了8组实验，得到如上表所示的实验数据．请利用表格数据，在如图c所示坐标系中描点做出相应图象．通过分析表中数据后，你得出a-F的图线是否呈线性变化，如果不是请分析其原因：a-F的图线不是一条直线，因为在以增加钩码质量m来增大拉力F的大小时，m越大，M＞＞m的实验条件越难以保证，所以a-F的图线会出现向F轴方向偏的情况．
（1）由图中刻度尺读出两个光电门中心之间的距离x=24cm，由图b中游标卡尺测得遮光条的宽度d=0.52 cm．该实验小组在做实验时，将滑块从如图a所示位置由静止释放，由数字计时器可以读出遮光条通过光电门1的时间△t1，遮光条通过光电门2的时间△t2，则滑块经过光电门1时的瞬时速度的表达式v1=$\frac{d}{△{t}_{1}}$，滑块经过光电门2时的瞬时速度的表达式v2=$\frac{d}{△{t}_{2}}$，则滑块的加速度的表达式a=$\frac{{（\frac{d}{△{t}_{2}}）}^{2}-{（\frac{d}{△{t}_{1}}）}^{2}}{2x}$．（用字母表示）
| F（N） | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 |
| a（m•s-2） | 0.06 | 0.11 | 0.18 | 0.26 | 0.30 | 0.36 | 0.40 | 0.43 |