��Ŀ����
18����ͼ����ʾ������ϵxOy�У���I�����ڳ�����ֱ����ƽ���������ǿ�ų����ڢ���������ˮƽ���Խ�����M��N��M��λ��x�������Ҷ���O���غϣ�������Ϊl�����峤��Ϊ2l��������ڽ����Դ�ϣ���Դ��ѹ��ʱ��仯�Ĺ�����ͼ�ң�M������������崦��һ����Դ������ˮƽ����������Ϊm�������Ϊq���ٶ�Ϊv0�Ĵ��������ӣ���֪t=0ʱ�̽����������ǡ������N����Ҷ������������P��2l��0���㣮�������������������Ӽ������ã����Խ��������Բ���֮��ĵ糡����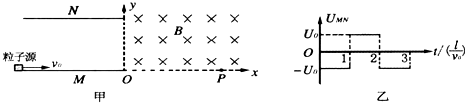
��1�������ĵ�ѹU0��
��2����ǿ�ų��ĴŸ�Ӧǿ��B��
��3��t=$\frac{l}{{4{v_0}}}$ʱ�̽���������ӣ�ͨ���ų�����x�ύ��ĺ����꣮
���� ��1��=0ʱ�̷����������ڰ���˶�ʱ����x�᷽�������˶�����y�᷽�������ȼ����˶��������ȼ����˶����������̵ļ��ٶȴ�С��ȣ�����������˶�ʱ����ȣ�����ţ�ٵڶ����ɺ��˶�ѧλ�ƹ�ʽ�г�y�����λ�Ʊ���ʽ��������⣮
��2�����ӽ���ų���������Բ���˶��������������ṩ���������ɼ��ι�ϵ����켣�뾶����ţ�ٵڶ�������B��
��3��t=$\frac{l}{{4{v_0}}}$ʱʱ�̽���������ӣ��ڡ�t1=$\frac{l}{{v}_{0}}$-$\frac{l}{4{v}_{0}}$=$\frac{3l}{4{v}_{0}}$ʱ������y������٣��ڽ������ġ�t2=$\frac{3l}{4{v}_{0}}$ʱ������-y������٣����ٶȼ�СΪ0��Ȼ���ڡ�t3=$\frac{l}{4{v}_{0}}$ʱ���ڣ���-y������٣����������ġ�t4=$\frac{l}{4{v}_{0}}$����-y�������Ϊ0��ǡ�õ���y�Ტ���ٶ�v0��ֱ��y���뿪�糡�����˶����̵ĶԳ��Ժͼ��ι�ϵ��⣮
���  �⣺��1��t=0ʱ�̷����������ڰ���˶�ʱ����x�᷽�������˶�������ʱ��Ϊ��
�⣺��1��t=0ʱ�̷����������ڰ���˶�ʱ����x�᷽�������˶�������ʱ��Ϊ��
t=$\frac{2l}{{v}_{0}}$����
��y�᷽�������ȼ����˶��������ȼ����˶����������̵ļ��ٶȴ�С��ȣ���Ϊ��a=$\frac{q{U}_{0}}{ml}$����
����N��ʱ��y����ķ��ٶ�Ϊ��
vy=a$\frac{l}{{v}_{0}}$-a$\frac{l}{{v}_{0}}$=0����
�����˶����̵ĶԳ��Կ�֪ǰ�������̵�λ����ȣ����У�
l=2��$\frac{1}{2}a��\frac{l}{{v}_{0}}��^{2}$����
�����ã�U0=$\frac{m{v}_{0}^{2}}{q}$����
��2�������ڴų����˶�ʱ�У�qv0B=m$\frac{{v}_{0}^{2}}{R}$����
�ɼ��ι�ϵ֪����2l��2+��R-l��2=R2����
��ã�B=$\frac{2m{v}_{0}}{5ql}$����
��3��t=$\frac{l}{{4{v_0}}}$ʱʱ�̽���������ӣ��ڡ�t1=$\frac{l}{{v}_{0}}$-$\frac{l}{4{v}_{0}}$=$\frac{3l}{4{v}_{0}}$ʱ������y������٣��ڽ������ġ�t2=$\frac{3l}{4{v}_{0}}$ʱ������-y������٣����ٶȼ�СΪ0��Ȼ���ڡ�t3=$\frac{l}{4{v}_{0}}$ʱ���ڣ���-y������٣����������ġ�t4=$\frac{l}{4{v}_{0}}$����-y�������Ϊ0��ǡ�õ���y�Ტ���ٶ�v0��ֱ��y���뿪�糡���������� y=2��$\frac{1}{2}a��{t}_{1}^{2}$=2��$\frac{1}{2}a��{t}_{3}^{2}$����
��� y=$\frac{l}{2}$����10��
�������ڴų����˶��뾶ҲΪR������ͨ��x��ʱ�ĺ�����Ϊx���ɼ��ι�ϵ֪
��R-$\frac{l}{2}$��2+x2=R2 ��11��
��ã�x=$\frac{3}{2}$l ��12��
�𣺣�1�������ĵ�ѹU0Ϊ$\frac{m{v}_{0}^{2}}{q}$��
��2����ǿ�ų��ĴŸ�Ӧǿ��BΪ$\frac{2m{v}_{0}}{5ql}$��
��3��t=$\frac{l}{{4{v_0}}}$ʱ�̽���������ӣ�ͨ���ų�����x�ύ��ĺ�����Ϊ$\frac{3}{2}$l��
���� ���������ڸ��ϳ����˶����ؼ�Ҫ��ȷ�������ӵ��˶���������ö���ѧ�����о��������ȱ���ֱ���˶�����ţ�ٵڶ����ɺ��˶�ѧ��ʽ��Ͻ�𣮶��ڴų�������Բ���˶��������켣�뾶����ϼ���֪ʶ���

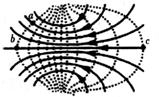
| A�� | c�㳡ǿ����a�㳡ǿ | |
| B�� | c����Ƹ���a����� | |
| C�� | c��b�����ĵ��Ʋ����c��a�����ĵ��Ʋ� | |
| D�� | ����һ��̽���+q��a���ƶ���b�㣬�糡�������� |
 �⻬ˮƽ���Ϸ�����������ͬ������ɣ��������д�������A��B��C���㣬��ͼ����ʾ��һ����m=1kg���������q=2C��С�����C���Ͼ�ֹ�ͷţ��侭��B��A������˶������ͼ����ʾ������B��Ϊ��-tͼ����б������λ�ã�ͼ�б���˹�B������ߣ��������·�����ȷ���ǣ�������
�⻬ˮƽ���Ϸ�����������ͬ������ɣ��������д�������A��B��C���㣬��ͼ����ʾ��һ����m=1kg���������q=2C��С�����C���Ͼ�ֹ�ͷţ��侭��B��A������˶������ͼ����ʾ������B��Ϊ��-tͼ����б������λ�ã�ͼ�б���˹�B������ߣ��������·�����ȷ���ǣ�������| A�� | B��Ϊ�д����ϵ糡ǿ�����ĵ��ҳ�ǿ��СE=1V/m | |
| B�� | ��C�㵽A�����ĵ������ȼ�С���� | |
| C�� | ��C�㵽A�㣬�������� | |
| D�� | B��A�����ĵ��Ʋ�ΪUBA=8.25V |
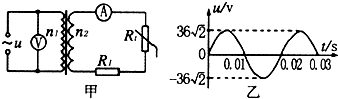
| A�� | �����ѹ��ԭ��Ȧ�Ľ�����ѹ�ı���ʽΪu=36$\sqrt{2}$sin50��tV | |
| B�� | ��ѹ��ԭ������Ȧ�еĵ���֮��Ϊ4��1 | |
| C�� | t=0.01sʱ�����������Ȧƽ��λ�������� | |
| D�� | R1�¶�����ʱ����ѹ�������빦�ʱ�С |
| A�� | mg$\sqrt{2gh}$ | B�� | mg$\sqrt{2gh}$cos�� | C�� | mg$\sqrt{2ghsin��}$ | D�� | mg$\sqrt{2gh}$sin�� |
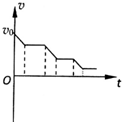
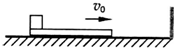 ��ͼ��ʾ���⻬ˮƽ������һ���γ�ľ�壬ľ����˷�һС��飬��֪ľ�������������������t=0ʱ���ߴ�ͼ��λ������ͬ��ˮƽ�ٶ�v0�����˶��������������ֱ�����ľ������ԭ���ȴ�����ٶȱ������������˶����������һֱδ�뿪ľ�壬���������˶����ٶ�v��ʱ��t�仯��ͼ�������ȷ���ǣ�������
��ͼ��ʾ���⻬ˮƽ������һ���γ�ľ�壬ľ����˷�һС��飬��֪ľ�������������������t=0ʱ���ߴ�ͼ��λ������ͬ��ˮƽ�ٶ�v0�����˶��������������ֱ�����ľ������ԭ���ȴ�����ٶȱ������������˶����������һֱδ�뿪ľ�壬���������˶����ٶ�v��ʱ��t�仯��ͼ�������ȷ���ǣ�������
 һ��������ΪM=60kg�����ĺ�Ⱥ��Բ������������ã����������Ϸ���ˮƽ���ϣ��������к�����ΪS=100cm2�Ĺ⻬��������������m=10kg�������ڷ����һ���������������壬��ʱ��������ΪL1=0.4m����֪����ѹΪpo=1��105Pa����������������������������ʹ�������뿪���棬���ĸ߶������Ƕ��٣���ȡ�������ٶ�g=l0m/s2����
һ��������ΪM=60kg�����ĺ�Ⱥ��Բ������������ã����������Ϸ���ˮƽ���ϣ��������к�����ΪS=100cm2�Ĺ⻬��������������m=10kg�������ڷ����һ���������������壬��ʱ��������ΪL1=0.4m����֪����ѹΪpo=1��105Pa����������������������������ʹ�������뿪���棬���ĸ߶������Ƕ��٣���ȡ�������ٶ�g=l0m/s2����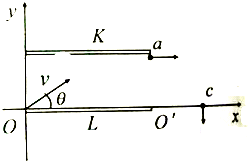 ��ͼ��ʾ����һƽ�а���������Ե��y���ϣ��¼�����x���غϣ��������ǿ�糡�ij�ǿΪE��һ����Ϊq������Ϊm�Ĵ������ӣ��ٶȴ�СΪ$\sqrt{3}$$\frac{E}{B}$����O����x��ɦȽ�б�������뼫��䣬���Ӿ���K���Եa��ƽ����x��ɳ�����������������һ�Ÿ�Ӧǿ��ΪB��Բ�δų���ͼ��δ����������c�㴹ֱ����x���뿪�ų�����֪��aco=45�㣬cos��=$\frac{\sqrt{3}}{3}$���ų�����ֱ������ƽ�����⣬�Ҵų�����������غϣ����������������ƣ�����
��ͼ��ʾ����һƽ�а���������Ե��y���ϣ��¼�����x���غϣ��������ǿ�糡�ij�ǿΪE��һ����Ϊq������Ϊm�Ĵ������ӣ��ٶȴ�СΪ$\sqrt{3}$$\frac{E}{B}$����O����x��ɦȽ�б�������뼫��䣬���Ӿ���K���Եa��ƽ����x��ɳ�����������������һ�Ÿ�Ӧǿ��ΪB��Բ�δų���ͼ��δ����������c�㴹ֱ����x���뿪�ų�����֪��aco=45�㣬cos��=$\frac{\sqrt{3}}{3}$���ų�����ֱ������ƽ�����⣬�Ҵų�����������غϣ����������������ƣ�����