题目内容
13.某行星自转一周所需时间为T,在这行星上用弹簧测力计可测得某物体的重力,在该行星赤道上称得物体的重力是两极的k倍,若该行星能够看作球体,求其平均密度(万有引力恒量为G).分析 两极处的万有引力等于物体的重力,赤道处的重力等于万有引力与物体绕行星自转所需的向心力之差,结合密度的表达式整理可得.
解答 解:在两极处物体受到的重力等于行星对它的万有引力,即:G$\frac{Mm}{{R}^{2}}$=F,
在赤道上的物体随星球自转做圆周运动,万有引力与重力之差提供向心力,
由牛顿第二定律得:G$\frac{Mm}{{R}^{2}}$-F′=m$(\frac{2π}{T})^{2}$R,
由题意可知:F′=kF,
行星的密度:ρ=$\frac{M}{V}$=$\frac{M}{\frac{4}{3}π{R}^{3}}$,
解得:ρ=$\frac{3π}{(1-k)G{T}^{2}}$;
答:行星的平均密度为$\frac{3π}{(1-k)G{T}^{2}}$.
点评 本题考查了万有引力定律的应用,知道赤道上的物体随行星做圆周运动的向心力来源,应用万有引力公式与牛顿第二定律可以解题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
3. 如图所示,两个固定的光滑半圆碗,半径分别为R1,R2且R1>R2,质量相等的A、B两小球,从碗的上边缘由静止滚下,碗的上边缘,在同一水平面上,设为零势位.下述正确的是( )
如图所示,两个固定的光滑半圆碗,半径分别为R1,R2且R1>R2,质量相等的A、B两小球,从碗的上边缘由静止滚下,碗的上边缘,在同一水平面上,设为零势位.下述正确的是( )
 如图所示,两个固定的光滑半圆碗,半径分别为R1,R2且R1>R2,质量相等的A、B两小球,从碗的上边缘由静止滚下,碗的上边缘,在同一水平面上,设为零势位.下述正确的是( )
如图所示,两个固定的光滑半圆碗,半径分别为R1,R2且R1>R2,质量相等的A、B两小球,从碗的上边缘由静止滚下,碗的上边缘,在同一水平面上,设为零势位.下述正确的是( )| A. | 小球由静止滚下,在达最低点P过程中,小球受到的合外力总是指向圆心 | |
| B. | 两小球达到最低点P时,对碗的压力相同 | |
| C. | 两小球在最低点P时,机械能相等 | |
| D. | 两小球达最低点P时速度相同 |
4.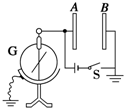 如图所示,电路中A、B为两块竖直放置的金属板,G是一只静电计,开关S合上后,静电计指针张开一个角度,下述做法可使指针张角增大的是( )
如图所示,电路中A、B为两块竖直放置的金属板,G是一只静电计,开关S合上后,静电计指针张开一个角度,下述做法可使指针张角增大的是( )
 如图所示,电路中A、B为两块竖直放置的金属板,G是一只静电计,开关S合上后,静电计指针张开一个角度,下述做法可使指针张角增大的是( )
如图所示,电路中A、B为两块竖直放置的金属板,G是一只静电计,开关S合上后,静电计指针张开一个角度,下述做法可使指针张角增大的是( )| A. | 使A、B两板靠近一些 | B. | 使A、B两板正对面积错开一些 | ||
| C. | 断开S后,使A板向左平移拉开一些 | D. | 断开S后,使A、B正对面积错开一些 |
1. 将一小球从高处水平抛出,最初2s内小球动能Ek随时间t变化的图线如图所示,不计空气阻力,重力加速度g=10m/s2.根据图象信息,不能确定的物理量是( )
将一小球从高处水平抛出,最初2s内小球动能Ek随时间t变化的图线如图所示,不计空气阻力,重力加速度g=10m/s2.根据图象信息,不能确定的物理量是( )
 将一小球从高处水平抛出,最初2s内小球动能Ek随时间t变化的图线如图所示,不计空气阻力,重力加速度g=10m/s2.根据图象信息,不能确定的物理量是( )
将一小球从高处水平抛出,最初2s内小球动能Ek随时间t变化的图线如图所示,不计空气阻力,重力加速度g=10m/s2.根据图象信息,不能确定的物理量是( )| A. | 小球的质量 | |
| B. | 小球的初速度 | |
| C. | 小球抛出时的高度 | |
| D. | 最初2 s内重力对小球做功的平均功率 |
18.两小球a,b在光滑的水平面上相向运动,碰撞后a球变为静止,b球仍然运动,则碰撞前( )
| A. | a球的动量大于b球的动量 | B. | b球的动量大于a球的动量 | ||
| C. | a球的速度大于b球的速度 | D. | b球的速度大于a球的速度 |
5.关于摩擦力的有关说法,正确的是( )
| A. | 摩擦力的大小一定与接触面上的压力成正比 | |
| B. | 运动物体受到的摩擦力一定等于μFN | |
| C. | 在水平面上的物体受到的摩擦力一定与该物体的重力大小成正比 | |
| D. | 以上说法都不正确 |
2.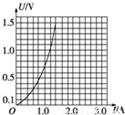 如图所示为小灯泡的U-I图线,若将该小灯泡与一节电动势E=1.5V,内阻r=0.75Ω的干电池组成闭合电路时,电源的总功率和小灯泡的实际电功率分别接近以下哪一组数据( )
如图所示为小灯泡的U-I图线,若将该小灯泡与一节电动势E=1.5V,内阻r=0.75Ω的干电池组成闭合电路时,电源的总功率和小灯泡的实际电功率分别接近以下哪一组数据( )
 如图所示为小灯泡的U-I图线,若将该小灯泡与一节电动势E=1.5V,内阻r=0.75Ω的干电池组成闭合电路时,电源的总功率和小灯泡的实际电功率分别接近以下哪一组数据( )
如图所示为小灯泡的U-I图线,若将该小灯泡与一节电动势E=1.5V,内阻r=0.75Ω的干电池组成闭合电路时,电源的总功率和小灯泡的实际电功率分别接近以下哪一组数据( )| A. | 1.5 W 1.0 W | B. | 0.75 W 0.5 W | C. | 0.75 W 0.75 W | D. | 1.5 W 0.75 W |
3. 2013年斯诺克上海沃德大师赛于9月16日至22日在上海体育馆举行.如图为丁俊晖正在准备击球,设丁俊晖在这一杆中,白色球(主球)和花色球碰撞前后都在同一直线上运动,碰前白色球的动量为pA=5kg•m/s,花色球静止,白球A与花色球B发生碰撞后,花色球B的动量变为pB′=4kg•m/s,则两球质量mA与mB间的关系可能是( )
2013年斯诺克上海沃德大师赛于9月16日至22日在上海体育馆举行.如图为丁俊晖正在准备击球,设丁俊晖在这一杆中,白色球(主球)和花色球碰撞前后都在同一直线上运动,碰前白色球的动量为pA=5kg•m/s,花色球静止,白球A与花色球B发生碰撞后,花色球B的动量变为pB′=4kg•m/s,则两球质量mA与mB间的关系可能是( )
 2013年斯诺克上海沃德大师赛于9月16日至22日在上海体育馆举行.如图为丁俊晖正在准备击球,设丁俊晖在这一杆中,白色球(主球)和花色球碰撞前后都在同一直线上运动,碰前白色球的动量为pA=5kg•m/s,花色球静止,白球A与花色球B发生碰撞后,花色球B的动量变为pB′=4kg•m/s,则两球质量mA与mB间的关系可能是( )
2013年斯诺克上海沃德大师赛于9月16日至22日在上海体育馆举行.如图为丁俊晖正在准备击球,设丁俊晖在这一杆中,白色球(主球)和花色球碰撞前后都在同一直线上运动,碰前白色球的动量为pA=5kg•m/s,花色球静止,白球A与花色球B发生碰撞后,花色球B的动量变为pB′=4kg•m/s,则两球质量mA与mB间的关系可能是( )| A. | mB=mA | B. | mB=$\frac{1}{4}$mA | C. | mB=$\frac{1}{6}$mA | D. | mB=6mA |