题目内容
(10分)从粒子源射出的带电粒子的质量为m、电荷量为q,它以速度v0经过电势差为U的带窄缝的平行板电极S1和S2间的电场,并从O点沿Ox方向进入磁感应强度为B、方向垂直纸面向外的有界匀强磁场,Ox垂直平行板电极S2,当粒子从P点离开磁场时,其速度方向与Ox方向的夹角θ=60°,如图8-2-20所示,整个装置处于真空中.
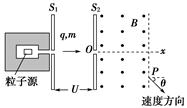
(1)求粒子在磁场中沿圆弧运动的轨道半径R;
(2)求粒子在磁场中运动所用的时间t.

(1)求粒子在磁场中沿圆弧运动的轨道半径R;
(2)求粒子在磁场中运动所用的时间t.
(1) (2)
(2)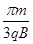
 (2)
(2)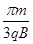
试题分析:(1)粒子进入平行板中的匀强电场,则电场力对其加速,利用动能定理则:
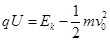
所以出电场的末速度为
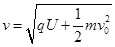
根据洛伦兹力提供向心力有
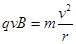 ,即
,即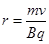 ,带入则
,带入则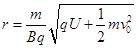
(2)

根据粒子在磁场中的运动轨迹可知,在磁场中轨迹的圆心角为60°。即
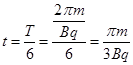
点评:此类题型属于比较常规型的带电粒子在电场或者磁场中的运动问题。根据动能定理可以求出在电场中加速后的末速度。通过左手定则定圆心,画轨迹,从而根据几何知识判断出半径。

练习册系列答案
相关题目




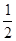 处返回,则下述措施能满足要求的是:( )
处返回,则下述措施能满足要求的是:( )