题目内容
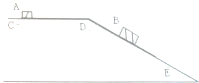
3．
如图所示，AB为一斜面，小球从A处以v0水平抛出，落地点恰在B点，已θ=30°，斜面长为L=10m，求小球在空中的飞行时间和小球平抛的初速度． g=10m/s2．
分析 平抛运动在水平方向上做匀速直线运动，竖直方向上做自由落体运动，根据下降的高度求出运动的时间，结合水平位移和时间求出小球的初速度．
解答 解：根据Lsin30°=$\frac{1}{2}g{t}^{2}$得，平抛运动的时间为：t=$\sqrt{\frac{2Lsin30°}{g}}=\sqrt{\frac{10}{10}}=1s$，
则平抛运动的初速度为：${v}_{0}=\frac{Lcos30°}{t}=5\sqrt{3}m/s$
答：小球在空中的飞行时间为1s，小球平抛的初速度为$5\sqrt{3}m/s$．
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律，知道平抛运动的时间由高度决定，初速度和时间共同决定水平位移．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
13．
如图所示，相同的乒乓球1、2落台后恰好在等高处水平越过竖直球网，过网时的速度方向均垂直于球网．不计乒乓球的旋转和空气阻力，乒乓球自起跳到最高点的过程中，下列说法中正确的是（ ）
如图所示，相同的乒乓球1、2落台后恰好在等高处水平越过竖直球网，过网时的速度方向均垂直于球网．不计乒乓球的旋转和空气阻力，乒乓球自起跳到最高点的过程中，下列说法中正确的是（ ）| A． | 起跳时，球1的速率大于球2的速率 | |
| B． | 球1的速度变化率小于球2的速度变化率 | |
| C． | 球1的飞行时间大于球2的飞行时间 | |
| D． | 过网时球1的速度等于球2的速度 |
11．理发用的电吹风机中有电动机和电热丝，电动机带动风叶转动，电热丝给空气加热，得到热风将头发吹干．设电动机线圈的电阻为R1，它与电热丝的电阻R2相串联，接到电源上时，电吹风机两端电压为U，电流为I，消耗的电功率为P，则有（ ）
| A． | P=I2（R1+R2） | B． | P=IU | C． | P=$\frac{{U}^{2}}{（{R}_{1}+{R}_{2}）}$ | D． | P＞I2（Rl+R2） |
如图所示，光滑绝缘的细圆管弯成半径为R的半圆形，固定在竖直面内，管口B、C的连线是水平直径，现有一带正电小球（可视为质点）从B点正上方的A点自由下落，A、B两点间距离为4R，从小球进入管口开始，整个空间中突然加上一个匀强电场，电场力竖直向上的分力大小与重力大小相等，结果小球运动到管口C时对圆管的外壁压力为3mg．设小球运动过程中带电量没有改变，重力加速度为g，求：
15．两块水平放置的平行金属板，带等量异种电荷，一个带电油滴恰悬浮在平行板间．如果使油滴产生大小等于$\frac{g}{2}$的加速度，两板电荷量应是原来的（ ）
| A． | $\frac{1}{2}$倍 | B． | 2倍 | C． | $\frac{2}{3}$倍 | D． | $\frac{3}{2}$倍 |
2．
如图所示，CD为光滑水平面，DE为与CD平滑连接的光滑斜面．一轻质丝带跨在CD和DE面上．质量为m和M的物块A、B分别放在水平和倾斜丝带上（M＞m）．A、B与丝带之间的动摩擦因数相同．刚开始，用手托住B，使A、B均处于静止状态；现撤去手，在A没有离开丝带和水平面且B没有离开丝带和斜面之前，下列判断正确的是（ ）
如图所示，CD为光滑水平面，DE为与CD平滑连接的光滑斜面．一轻质丝带跨在CD和DE面上．质量为m和M的物块A、B分别放在水平和倾斜丝带上（M＞m）．A、B与丝带之间的动摩擦因数相同．刚开始，用手托住B，使A、B均处于静止状态；现撤去手，在A没有离开丝带和水平面且B没有离开丝带和斜面之前，下列判断正确的是（ ）| A． | A可能静止、B相对斜面下滑 | |
| B． | A、B的加速度大小可能相等 | |
| C． | A增加的机械能一定等于B减小的机械能 | |
| D． | A、B与丝带之间的摩擦力大小一定相等 |