题目内容
18.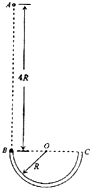 如图所示,光滑绝缘的细圆管弯成半径为R的半圆形,固定在竖直面内,管口B、C的连线是水平直径,现有一带正电小球(可视为质点)从B点正上方的A点自由下落,A、B两点间距离为4R,从小球进入管口开始,整个空间中突然加上一个匀强电场,电场力竖直向上的分力大小与重力大小相等,结果小球运动到管口C时对圆管的外壁压力为3mg.设小球运动过程中带电量没有改变,重力加速度为g,求:
如图所示,光滑绝缘的细圆管弯成半径为R的半圆形,固定在竖直面内,管口B、C的连线是水平直径,现有一带正电小球(可视为质点)从B点正上方的A点自由下落,A、B两点间距离为4R,从小球进入管口开始,整个空间中突然加上一个匀强电场,电场力竖直向上的分力大小与重力大小相等,结果小球运动到管口C时对圆管的外壁压力为3mg.设小球运动过程中带电量没有改变,重力加速度为g,求:(1)小球到达B点的速度大小:
(2)小球受到的电场力的大小和方向;
(3)小球从管口C处脱离圆管后,其运动轨迹经过AB连线上某点P,P点到B点的距离;
(4)小球到达P点的速度的大小和方向.
分析 (1)小球从A点自由下落过程,根据运动学公式求解B点的速度大小;
(2)小球经过C点时,由管壁的压力和电场力的水平分力的合力提供向心力,列式求解小球在C点受到的电场力的水平分力,再由力的合成求解电场力.
(3)小球从管口C处脱离圆管后,根据牛顿第二定律求小球水平分加速度,再由分位移公式求解.
(4)小球从C到P过程,根据动能定理列式求解.
解答 解:(1)从A到B,由vB2=2gh,h=4R
则 vB=2$\sqrt{2gR}$
(2)在C点,由牛顿第二定律得
3mg+Fx=m$\frac{{v}_{C}^{2}}{R}$
从B到C,由动能定理得:-Fx2R=$\frac{1}{2}$(m vc2-m vB2)
解得Fx=mg,vc=2$\sqrt{gR}$
据题 Fy=mg
故电场力大小为 F=$\sqrt{2}$ mg,方向与水平成45°斜向左上方
(3)从C运动到P过程,小球的水平分加速度 ax=$\frac{{F}_{x}}{m}$=g
水平方向有:
2R=$\frac{1}{2}$axt2
竖直方向有 y=vct
解得 y=4R
(4)根据动能定理得:
Fx•2R=$\frac{1}{2}$(m vP2-m vC2)
解得 vP=2$\sqrt{2gR}$,方向与水平成45°斜向左上方.
答:
(1)小球到达B点的速度大小是2$\sqrt{2gR}$:
(2)小球受到的电场力的大小是$\sqrt{2}$ mg,方向与水平成45°斜向左上方;
(3)小球从管口C处脱离圆管后,其运动轨迹经过AB连线上某点P,P点到B点的距离是4R;
(4)小球到达P点的速度的大小2$\sqrt{2gR}$,方向与水平成45°斜向左上方.
点评 本题关键运用正交分解法,将小球的运动沿水平方向和竖直方向正交分解,然后运用牛顿运动定律和动能定理列式解答.

| A. | 一个物体所受的合外力为零,它的机械能一定守恒 | |
| B. | 一个物体做匀速运动,它的机械能一定守恒 | |
| C. | 一个物体所受的合外力不为零,它的机械能可能守恒 | |
| D. | 一个物体所受合外力的功为零,它不一定保持静止或匀速直线运动 |
| A. | 光的偏振现象说明光是纵波 | |
| B. | 对衍射现象的研究表明,我们一般所说的“光沿直线传播”只是一种特殊情况 | |
| C. | 牛顿的“微粒说”、惠更斯的“波动说”、爱因斯坦提出了“光子说”都圆满地说明了光的本性 | |
| D. | 电磁波中每一处的电场强度和磁感应强度都与波的传播方向垂直 |
| A. | v1>v2,△E1=△E2 | B. | v1>v2,△E1<△E2 | C. | v1=v2,△E1=△E2 | D. | v1<v2,△E1<△E2 |
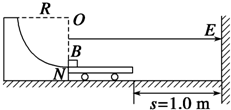 如图所示,半径为R=0.2m,光滑绝缘的$\frac{1}{4}$圆弧轨道固定在光滑水平地面上.轨道末端水平,紧靠轨道末端有一等高的绝缘平板小车,小车表面水平,车长L=1m,质量为2M,车子右端与竖直绝缘挡板的距离为s=1.0m.轨道末端右侧空间存在水平向右、大小为E=$\frac{3μMg}{q}$的匀强电场.质量为M=1kg、不带电的滑块B静止在小车的左端.质量也为M、带电荷量为q的滑块A(A、B均可看作质点,图中A未画出),从轨道上的某一点由静止释放,通过轨道末端N点时对轨道的压力为A重力的3倍,与滑块B碰撞后粘合在一起,碰撞过程中无电荷量损失.A、B滑块与平板车间的动摩擦因数为μ=0.2,车与挡板碰后立即被锁定.A、B粘合后与挡板碰撞过程中无能量损失,且不计电荷量损失.(g=10m/s2)求:
如图所示,半径为R=0.2m,光滑绝缘的$\frac{1}{4}$圆弧轨道固定在光滑水平地面上.轨道末端水平,紧靠轨道末端有一等高的绝缘平板小车,小车表面水平,车长L=1m,质量为2M,车子右端与竖直绝缘挡板的距离为s=1.0m.轨道末端右侧空间存在水平向右、大小为E=$\frac{3μMg}{q}$的匀强电场.质量为M=1kg、不带电的滑块B静止在小车的左端.质量也为M、带电荷量为q的滑块A(A、B均可看作质点,图中A未画出),从轨道上的某一点由静止释放,通过轨道末端N点时对轨道的压力为A重力的3倍,与滑块B碰撞后粘合在一起,碰撞过程中无电荷量损失.A、B滑块与平板车间的动摩擦因数为μ=0.2,车与挡板碰后立即被锁定.A、B粘合后与挡板碰撞过程中无能量损失,且不计电荷量损失.(g=10m/s2)求: 如图所示为频闪摄影方法拍摄的研究物体做平抛运动规律的照片,图中A、B、C为三个同时由同一点出发的小球.AA′为A球在光滑水平面上以速度v运动的轨迹;BB′为B球以速度v被水平抛出后的运动轨迹;CC′为C球自由下落的运动轨迹.通过分析上述三条轨迹可得出结论:平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.
如图所示为频闪摄影方法拍摄的研究物体做平抛运动规律的照片,图中A、B、C为三个同时由同一点出发的小球.AA′为A球在光滑水平面上以速度v运动的轨迹;BB′为B球以速度v被水平抛出后的运动轨迹;CC′为C球自由下落的运动轨迹.通过分析上述三条轨迹可得出结论:平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.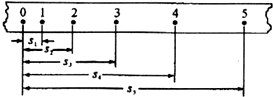 (1)利用重锤的自由下落验证机械能守恒定律,下面哪些测量工具是必需的?C.
(1)利用重锤的自由下落验证机械能守恒定律,下面哪些测量工具是必需的?C. 如图所示,AB为一斜面,小球从A处以v0水平抛出,落地点恰在B点,已θ=30°,斜面长为L=10m,求小球在空中的飞行时间和小球平抛的初速度. g=10m/s2.
如图所示,AB为一斜面,小球从A处以v0水平抛出,落地点恰在B点,已θ=30°,斜面长为L=10m,求小球在空中的飞行时间和小球平抛的初速度. g=10m/s2. 如图所示,是小球平抛运动过程中拍下的频闪照片中的一部分.已知频闪周期为T,照片中每个背景小正方形的边长所代表的实际长度为b.则小球平抛的初速度大小v0=$\frac{3b}{T}$,重力加速度g=$\frac{b}{{T}^{2}}$.(以上两空均用用b、T表示.)
如图所示,是小球平抛运动过程中拍下的频闪照片中的一部分.已知频闪周期为T,照片中每个背景小正方形的边长所代表的实际长度为b.则小球平抛的初速度大小v0=$\frac{3b}{T}$,重力加速度g=$\frac{b}{{T}^{2}}$.(以上两空均用用b、T表示.)