题目内容
14．
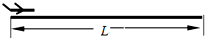如图所示，航空母舰上的水平起飞跑道长度L=160m．一架质量为m=2.0×104kg的飞机从跑道的始端开始，在大小恒为F=1.2×105N的动力作用下，飞机做初速度为零的匀加速直线运动，在运动过程中飞机受到的平均阻力大小为Ff=2×104N．飞机可视为质点，取g=10m/s2．求：（1）飞机在水平跑道运动的加速度大小；
（2）若航空母舰静止不动，飞机加速到跑道末端时速度大小．
分析 根据牛顿第二定律求出飞机在水平跑道上运动的加速度大小，结合速度位移公式求出飞机加速到跑道末端的速度大小．
解答 解：（1）根据牛顿第二定律得，飞机在水平跑道上的加速度a=$\frac{F-{F}_{f}}{m}=\frac{1.2×1{0}^{5}-2×1{0}^{4}}{2×1{0}^{4}}=5m/{s}^{2}$．
（2）根据速度位移公式得，v2=2aL，
解得v=$\sqrt{2aL}=\sqrt{2×5×160}$m/s=40m/s．
答：（1）飞机在水平跑道运动的加速度大小为5m/s2；
（2）飞机加速到跑道末端的速度大小为40m/s．
点评 本题考查了牛顿第二定律和运动学公式的基本运用，知道加速度是联系力学和运动学的桥梁，基础题．
练习册系列答案
相关题目
4．在力的合成中，下列关于两个分力与它们的合力关系的说法中，正确的是（ ）
| A． | 合力一定大于每一个分力 | |
| B． | 合力一定小于每一个分力 | |
| C． | 两个分力大小不变，夹角在0°～180°之间变化时，夹角越大合力越小 | |
| D． | 两个分力大小不变，夹角在0°～180°之间变化时，夹角越大合力越大 |
2．
如图两根光滑的杆互相垂直的固定在一起，上面分别穿有一个小球，小球a、b间用一细直棒相连，当细直棒与竖直杆夹角为θ时，两小球实际速度大小之比是（ ）
如图两根光滑的杆互相垂直的固定在一起，上面分别穿有一个小球，小球a、b间用一细直棒相连，当细直棒与竖直杆夹角为θ时，两小球实际速度大小之比是（ ）| A． | sinθ | B． | cosθ | C． | tanθ | D． | $\frac{1}{tanθ}$ |
19．
-个带电圆金属环绕其轴OO′转动时，放置在左面轴线上的小磁针N极静止时的指向如图图示，圆环的带电情况和旋转方向是（ ）
-个带电圆金属环绕其轴OO′转动时，放置在左面轴线上的小磁针N极静止时的指向如图图示，圆环的带电情况和旋转方向是（ ）| A． | 如从左往右看，正电，顺时针 | B． | 如从左往右看，负电，逆时针 | ||
| C． | 如从右往左看，正电，顺时针 | D． | 如从右往左看，负电，顺时针 |
2．
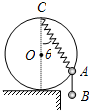如图所示，两个质量均为m的小球A、B用不可伸长的轻绳连接，A球穿在一光滑圆环上，轻质弹簧的一端固定在圆环最高点C，另一端连接A球，圆环竖直固定在水平面上，系统处于静止状态，发生弹性形变的弹簧与竖直方向的夹角θ=30°．现剪断A、B两球间的轻绳，在剪断轻绳的瞬间，A球的加速度大小为（ ）
如图所示，两个质量均为m的小球A、B用不可伸长的轻绳连接，A球穿在一光滑圆环上，轻质弹簧的一端固定在圆环最高点C，另一端连接A球，圆环竖直固定在水平面上，系统处于静止状态，发生弹性形变的弹簧与竖直方向的夹角θ=30°．现剪断A、B两球间的轻绳，在剪断轻绳的瞬间，A球的加速度大小为（ ）| A． | $\frac{\sqrt{3}}{2}$g | B． | $\frac{\sqrt{3}}{3}$g | C． | g | D． | 0 |
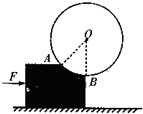如图所示，一圆柱体放在带有弧形凹槽的滑块上，且圆柱体的半径与弧形凹槽的半径相同，∠AOB=45°，圆柱体的质量为m，滑块的质量为M，滑块与地面间的动摩擦因数为μ，现用力F推着滑块保证圆柱体与其一起水平向右运动．求：