题目内容
【题目】如图所示,固定的倾斜粗糙细杆与水平地面间的夹角为θ=37°,质量为1.0kg的圆环套在细杆.细质弹簧的一端固定在水平地面上的O点,另一端与圆环相连接,当圆环在A点时弹簧恰好处于原长状态且与轻杆垂直.将圆环从A点由静止释放,滑到细杆的底端C点时速度为零.若圆环在C点获得沿细杆向上且大小等于2.0m/s的初速度,则圆环刚好能再次回到出发点A.已知B为AC的中点,弹簧原长为0.3m,在圆环运动过程中弹簧始终在弹性限度内,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.( )

A. 下滑过程中,圆环受到的合力一直在增大
B. 下滑过程中,圆环与细杆摩擦产生的热量为1.0J
C. 在圆环从C点回到A点的过程中,弹簧对圆环做的功为1.2J
D. 圆环下滑经过B点的速度一定小于上滑时经过B点的速度
【答案】BD
【解析】下滑过程中,圆环受到重力、弹簧的弹力和杆的支持力,弹簧的弹力逐渐增大,可知合力先减小后增大,故A错误.设下滑过程中,圆环与细杆摩擦产生的热量为Q,上滑时产生的热量也为Q.由能量守恒定律得:下滑过程有 Q+Ep=mgh;上滑过程有![]() ,解得
,解得![]() ,故B正确.由上得 Ep=mgh-Q=1×10×0.3×sin53°-2=0.4J,故C错误.从C到B,由动能定理得:
,故B正确.由上得 Ep=mgh-Q=1×10×0.3×sin53°-2=0.4J,故C错误.从C到B,由动能定理得:
-WF-Wf+![]() mgh=
mgh=![]() m
m![]() -0;从B到C,由动能定理得:
-0;从B到C,由动能定理得: ![]()
对比可得 vB1<vB2,即圆环下滑经过B点的速度一定小于上滑时经过B点的速度,故D正确.故选BD.

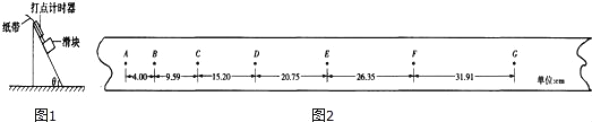
【题目】某实验小组欲以如图1所示实验装置探究“加速度与物体受力和质量的关系”.图1中A为小车,B为装有砝码的小盘,C为一端带有定滑轮的长木板,小车通过纸带与电磁打点计时器相连,小车的质量为m1,小盘(及砝码)的质量为m2.

(1)下列说法正确的是
A.实验时先放开小车,再接通打点计时器的电源 |
B.每次改变小车质量时,应重新平衡摩擦力 |
C.本实验中应满足m2远小于m1的条件 |
D.在用图象探究小车加速度与受力的关系时,应作a﹣m1图象 |
(2)实验中得到一条打点的纸带,如图2所示,已知相邻计数点间的时间间隔为T,且间距x1、x2、x3、x4、x5、x6已量出,则打点计时器打下F点时小车的瞬时速度的计算式为vF= ,小车加速度的计算式a= .