题目内容
19.天文学家发现某恒星有一颗行星在圆形轨道上绕其运动,并测出了行星的轨道半径R和公转周期T,已知引力常量为G,由此可算出( )| A. | 恒星质量 | B. | 恒星平均密度 | C. | 行星质量 | D. | 行星半径 |
分析 行星绕恒星做圆周运动,万有引力提供向心力,由牛顿第二定律列方程解题.
解答 解:AC、设恒星的质量为M,行星的质量为m,行星绕恒星做圆周运动,万有引力提供向心力,由牛顿第二定律得:G$\frac{Mm}{{R}^{2}}$=m$(\frac{2π}{T})^{2}$R,解得:M=$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$,可以求出恒星的质量,但不能求出行星的质量,故A正确,C错误;
B、可以求出恒星的质量,但是由于不知道恒星的半径,不知道恒星的体积,无法求出恒星的平均密度,故B错误;
D、根据题意可以知道行星绕恒星运动的轨道半径,但不能求出行星的半径,故D错误;
故选:A.
点评 本题考查了万有引力定律的应用,应用万有引力定律与牛顿第二定律即可解题,本题是一道基础题.

练习册系列答案
相关题目
9.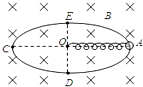 如图所示,竖直平面内有一固定的光滑绝缘椭圆大环,水平长轴为AC,竖直短轴为ED.轻弹簧一端固定在大环的中心O,另一端连接一个可视为质点的带正电的小环,小环刚好套在大环上,整个装置处在一个水平向里的匀强磁场中.将小环从A点由静止释放,已知小环在A、D两点时弹簧的形变量大小相等.下列说法中正确的是( )
如图所示,竖直平面内有一固定的光滑绝缘椭圆大环,水平长轴为AC,竖直短轴为ED.轻弹簧一端固定在大环的中心O,另一端连接一个可视为质点的带正电的小环,小环刚好套在大环上,整个装置处在一个水平向里的匀强磁场中.将小环从A点由静止释放,已知小环在A、D两点时弹簧的形变量大小相等.下列说法中正确的是( )
 如图所示,竖直平面内有一固定的光滑绝缘椭圆大环,水平长轴为AC,竖直短轴为ED.轻弹簧一端固定在大环的中心O,另一端连接一个可视为质点的带正电的小环,小环刚好套在大环上,整个装置处在一个水平向里的匀强磁场中.将小环从A点由静止释放,已知小环在A、D两点时弹簧的形变量大小相等.下列说法中正确的是( )
如图所示,竖直平面内有一固定的光滑绝缘椭圆大环,水平长轴为AC,竖直短轴为ED.轻弹簧一端固定在大环的中心O,另一端连接一个可视为质点的带正电的小环,小环刚好套在大环上,整个装置处在一个水平向里的匀强磁场中.将小环从A点由静止释放,已知小环在A、D两点时弹簧的形变量大小相等.下列说法中正确的是( )| A. | 刚释放时,小球的加速度为重力加速度g | |
| B. | 小环的质量越大,其滑到D点时的速度将越大 | |
| C. | 小环从A到运动到D,弹簧对小环做正功 | |
| D. | 小环一定不能滑到C点 |
10.两颗人造卫星绕地球做稳定的匀速圆周运动,它们的动能相等,它们的质量之比为1:4,则它们的( )
| A. | 半径之比为1:2 | B. | 速率之比为4:1 | C. | 周期之比为1:4 | D. | 向心力之比为4:1 |
14. 如图甲所示,线圈ABCD固定于匀强磁场中,磁场方向垂直纸面向里,当磁感应强度如图乙所示变化时,下列说法正确的是( )
如图甲所示,线圈ABCD固定于匀强磁场中,磁场方向垂直纸面向里,当磁感应强度如图乙所示变化时,下列说法正确的是( )
 如图甲所示,线圈ABCD固定于匀强磁场中,磁场方向垂直纸面向里,当磁感应强度如图乙所示变化时,下列说法正确的是( )
如图甲所示,线圈ABCD固定于匀强磁场中,磁场方向垂直纸面向里,当磁感应强度如图乙所示变化时,下列说法正确的是( )| A. | AB边所受安培力方向向左 | B. | AB边所受安培力方向向右 | ||
| C. | 边所受安培力大小可能不变 | D. | 边所受安培力大小一定变大 |
4. 在街头理发店门口,常可以看到这样的标志:一个转动的圆筒.外表面有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉.如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)L=30cm,若圆筒在1min内匀速转动20圈,我们观察到条纹以速度v向上匀速运动,则圆筒的转动方向(从上向下看)和v分别为( )
在街头理发店门口,常可以看到这样的标志:一个转动的圆筒.外表面有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉.如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)L=30cm,若圆筒在1min内匀速转动20圈,我们观察到条纹以速度v向上匀速运动,则圆筒的转动方向(从上向下看)和v分别为( )
 在街头理发店门口,常可以看到这样的标志:一个转动的圆筒.外表面有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉.如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)L=30cm,若圆筒在1min内匀速转动20圈,我们观察到条纹以速度v向上匀速运动,则圆筒的转动方向(从上向下看)和v分别为( )
在街头理发店门口,常可以看到这样的标志:一个转动的圆筒.外表面有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉.如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)L=30cm,若圆筒在1min内匀速转动20圈,我们观察到条纹以速度v向上匀速运动,则圆筒的转动方向(从上向下看)和v分别为( )| A. | 逆时针,v=0.1m/s | B. | 逆时针,v=0.9m/s | C. | 顺时针,v=0.1m/s | D. | 顺时针,v=0.9m/s |
11.两个物体A、B,以相同的速率V0在同一位置时向相反的方向水平抛出,经时间t,A的速度方向与B的位移方向相互垂直,则t为:( )
| A. | $\frac{{V}_{0}}{g}$ | B. | $\frac{2{V}_{0}}{g}$ | C. | $\frac{{V}_{0}}{2g}$ | D. | $\frac{\sqrt{2}{V}_{0}}{g}$ |
8.物体沿直线运动的位置坐标随时间变化的关系为x=(2+t)2,下列说法正确的是( )
| A. | 物体运动的加速度为2m/s2 | |
| B. | t=0时刻物体的速度为2m/s | |
| C. | 从t=0到t=2s时间内物体运动的位移为16m | |
| D. | 从t=0到t=2s时间内物体的平均速度为12m/s |
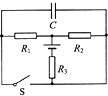 如图所示的电路中,Rl=3Ω,R2=6Ω,R3=1.5Ω,C=20?F,当开关S断开时,电源的总功率为2W,当开关S闭合时,电源的总功率为4W.求:
如图所示的电路中,Rl=3Ω,R2=6Ω,R3=1.5Ω,C=20?F,当开关S断开时,电源的总功率为2W,当开关S闭合时,电源的总功率为4W.求: 如图所示,将质量为3kg的小球水平抛出,空气阻力不计,求:
如图所示,将质量为3kg的小球水平抛出,空气阻力不计,求: