题目内容
8. 如图所示,光滑绝缘的水平面上有水平向右的匀强电场,电场强度E=2.0×104N/C,物块甲(不带电、可看做质点)在外力作用下从A点以a1=10m/s2的加速度由静止开始向右做匀加速运动,同时质量m=1.0×10-1kg、带电量为q=+2.0×10-5C,物块乙从B点以初速度v0向左匀减速运动,甲运动到C点时去掉外力作用,甲、乙开始运动时开始计时,t=1.0s时,两物块相遇,已知A、C两点间的距离s1=0.2m,B、C两点间的距离s2=4.0m,重力加速度g=10m/s2,求:
如图所示,光滑绝缘的水平面上有水平向右的匀强电场,电场强度E=2.0×104N/C,物块甲(不带电、可看做质点)在外力作用下从A点以a1=10m/s2的加速度由静止开始向右做匀加速运动,同时质量m=1.0×10-1kg、带电量为q=+2.0×10-5C,物块乙从B点以初速度v0向左匀减速运动,甲运动到C点时去掉外力作用,甲、乙开始运动时开始计时,t=1.0s时,两物块相遇,已知A、C两点间的距离s1=0.2m,B、C两点间的距离s2=4.0m,重力加速度g=10m/s2,求:(1)甲、乙两物块相遇的位置离C点的距离;
(2)物块乙的初速度v0的大小.
分析 (1)由速度和位移公式可求得速度;再由速度和时间关系可求得时间,由匀速直线运动规律可求得位移;
(2)由电场强度可求得电场力,再由牛顿第二定律可求得加速度;由相遇的条件可求得初速度.
解答 解:(1)设物块甲到C点时的速度为v1,由运动规律得:
v12=2a1s
代入数据解得:v1=2.0m/s
物块甲到C点所用的时间为:t1=$\frac{{v}_{1}}{{a}_{1}}$=$\frac{2}{10}$=0.2s
所以两物块相遇的位置在C点右侧,有:x=v1(t-t1)=2×(1-0.2)=1.6m
(2)设物块乙运动的加速度为a2,由牛顿第二定律得:
qE=ma2
得:a2=$\frac{Eq}{m}$=$\frac{2×1{0}^{-5}×2×1{0}^{4}}{1×1{0}^{-1}}$m/s2=4.0m/s2
由运动规律得:s2-x=v0t-$\frac{1}{2}$a2t2
代入数据解得:v0=4.4m/s
答:(1)甲、乙两物块相遇的位置离C点的距离为1.6m
(2)物块乙的初速度v0的大小为4.4m/s
点评 本题考查牛顿第二定律及运动学公式的应用,要注意正确分析两物体的运动及受力情况,由牛顿第二定律可分析求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.快热式电热水器,也叫即热电热水器,它无需巨大的储水桶,不需预热和保温.通电通水后打开出水口几秒种就会流出热水,即开、即热、即用、即停,省时、省电、省水、省空间,因此有逐渐替代储水式电热水器的趋势.如表是某快热式电热水器的铭牌,求该电热水器正常工作时:
(1)通过电热水器的电流;
(2)电热水器工作100s产生的热量.
| 快热式电热水器 | |
| 型号 | DSF-S6-80 |
| 额定电压 | 220V~ |
| 额定频率 | 50Hz |
| 额定功率 | 8800W |
| 额定压力 | 0.6Mpa |
| 防水等级 | LPX 4 |
(2)电热水器工作100s产生的热量.
19.假设地球是一半径为R,质量分布均匀的球体.假设一矿井深度为d=$\frac{R}{2}$,已知质量分布均匀的球壳对壳内物体的引力为零.矿井底部和地面处的重力加速度大小之比为( )
| A. | 4 | B. | $\frac{1}{4}$ | C. | 2 | D. | $\frac{1}{2}$ |
16.关于永动机和热力学定律的讨论,系列叙述正确的是 ( )
| A. | 第二类永动机违反能量守恒定律 | |
| B. | 热量不可能自发地从低温物体传到高温物体 | |
| C. | 对某物体做功,物体的内能必定增加 | |
| D. | 可以从单一热源吸收热量,使之完全变为功 | |
| E. | 能量耗散从能量转化角度反映出自然界中的宏观过程具有方向性 |
3.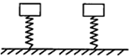 如图所示,两根完全相同的轻质弹簧,下端固定在地面上,质量不同、形状相同的两物块分别置于两弹簧上端但不栓接,现用外力作用在物体上,使两弹簧具有相同的压缩量,撤去外力后,两物块由静止向上运动并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块一定满足(弹簧始终在弹性限度之内,以地面为零势能面)( )
如图所示,两根完全相同的轻质弹簧,下端固定在地面上,质量不同、形状相同的两物块分别置于两弹簧上端但不栓接,现用外力作用在物体上,使两弹簧具有相同的压缩量,撤去外力后,两物块由静止向上运动并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块一定满足(弹簧始终在弹性限度之内,以地面为零势能面)( )
 如图所示,两根完全相同的轻质弹簧,下端固定在地面上,质量不同、形状相同的两物块分别置于两弹簧上端但不栓接,现用外力作用在物体上,使两弹簧具有相同的压缩量,撤去外力后,两物块由静止向上运动并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块一定满足(弹簧始终在弹性限度之内,以地面为零势能面)( )
如图所示,两根完全相同的轻质弹簧,下端固定在地面上,质量不同、形状相同的两物块分别置于两弹簧上端但不栓接,现用外力作用在物体上,使两弹簧具有相同的压缩量,撤去外力后,两物块由静止向上运动并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块一定满足(弹簧始终在弹性限度之内,以地面为零势能面)( )| A. | 两物块达最大速度时的高度相同 | B. | 上升的最大高度不同 | ||
| C. | 最大加速度相同 | D. | 最大重力势能不同 |
13. 如图所示,氢原子可在下列各能级间发生跃迁,设从n=4到n=1能级辐射的电磁波的波长为λ1,从n=4到n=2能级辐射的电磁波的波长为λ2,从n=2到n=1能级辐射的电磁波的波长为λ3,则下列关系式中正确的是( )
如图所示,氢原子可在下列各能级间发生跃迁,设从n=4到n=1能级辐射的电磁波的波长为λ1,从n=4到n=2能级辐射的电磁波的波长为λ2,从n=2到n=1能级辐射的电磁波的波长为λ3,则下列关系式中正确的是( )
 如图所示,氢原子可在下列各能级间发生跃迁,设从n=4到n=1能级辐射的电磁波的波长为λ1,从n=4到n=2能级辐射的电磁波的波长为λ2,从n=2到n=1能级辐射的电磁波的波长为λ3,则下列关系式中正确的是( )
如图所示,氢原子可在下列各能级间发生跃迁,设从n=4到n=1能级辐射的电磁波的波长为λ1,从n=4到n=2能级辐射的电磁波的波长为λ2,从n=2到n=1能级辐射的电磁波的波长为λ3,则下列关系式中正确的是( )| A. | λ1<λ3 | B. | λ3<λ2 | C. | λ3>λ2 | D. | $\frac{1}{{λ}_{3}}$=$\frac{1}{{λ}_{1}}$+$\frac{1}{{λ}_{2}}$ | ||||
| E. | $\frac{1}{{λ}_{3}}$=$\frac{1}{{λ}_{1}}$-$\frac{1}{{λ}_{2}}$ |
20.如图所示,两束单色光a,b射向水面A点,经折射后组成一束复色光,则( )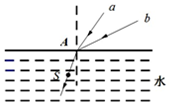

| A. | 在水中a光的速度比b光的速度小 | |
| B. | 以水下S点为光源向水面发射复色光,a光更容易发生全反射 | |
| C. | 用同一双缝干涉实验装置做实验,a光的干涉条纹间距大于b光的间距 | |
| D. | 若a、b两束光的入射角均增加相同角度,经水的折射后仍能组成一束复色光 |
17.宇航员在月球表面以初速度v0将一石块与水平方向成θ角斜向上抛出,小球上升的最大高度为h,月球的半径为R,引力常量为G.由此可推算( )
| A. | 月球表面的重力加速度为$\frac{{{v}_{0}}^{2}co{s}^{2}θ}{2h}$ | |
| B. | 月球的质量为$\frac{{{v}_{0}}^{2}{R}^{2}si{n}^{2}θ}{2Gh}$ | |
| C. | 石块在空中的运动时间为$\frac{2h}{{v}_{0}sinθ}$ | |
| D. | 月球的第一宇宙速度为v0sinθ$\sqrt{\frac{R}{h}}$ |
18.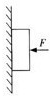 如图所示,用力F把木块紧压在竖直墙上不动,木块对墙的压力为N木块受到的摩擦力为f,到的重力为G,则( )
如图所示,用力F把木块紧压在竖直墙上不动,木块对墙的压力为N木块受到的摩擦力为f,到的重力为G,则( )
 如图所示,用力F把木块紧压在竖直墙上不动,木块对墙的压力为N木块受到的摩擦力为f,到的重力为G,则( )
如图所示,用力F把木块紧压在竖直墙上不动,木块对墙的压力为N木块受到的摩擦力为f,到的重力为G,则( )| A. | N>F | B. | N<F | C. | f>G | D. | f=G |