Question

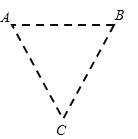
【题目】一三棱柱形玻璃砖的横截面如图所示，∠A＝90°、∠C＝60°，已知AC＝l，玻璃砖的折射率为n＝。一细光束从AB边的中点沿与AB边成45°角的方向射入玻璃砖。已知光在真空中的速度为c。

(ⅰ)分析光能否从BC边射出，并说明理由；

(ⅱ)不考虑原路返回的光线，光通过玻璃砖所用时间为多少？

Answer 1

【答案】(ⅰ)根据已知条件得C＝45°，因为θ＝60°>C，所以光在E点发生全反射，不能从BC边射出。(ⅱ)

【解析】

根据“光能否从BC边射出”、“光通过玻璃砖所用时间为多少”可知，本题考查全反射和折射定律，根据全反射规律求出临界角，根据折射定律求出折射角和光在玻璃中通过的距离，即可进行计算。

(ⅰ)作出光路图如图所示：

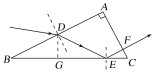
设折射光线与BC的交点为E，光束在D点发生折射时，入射角为i，折射角为r，由折射定律有

代入数据解得r＝30°

由几何关系可知，光在E点的入射角θ＝60°

设全反射的临界角为C，则sin C＝

根据已知条件得C＝45°，因为θ>C，所以光在E点发生全反射，不能从BC边射出。

(ⅱ)设光线的出射点为F，由几何关系可知光线垂直AC边射出玻璃砖

过D点作BC边的垂线且垂足为G，

由几何关系得BC＝2l，AB＝l

CE＝2l－2BG，BG＝ABcos 30°

解得CE＝，DE＝BD

光在玻璃砖中的行程为

x＝DE＋EF＝BD＋CEcos 30°＝l

光在玻璃砖中的速度为v＝＝c

则光通过玻璃砖的时间为t＝＝。