题目内容
(2007?上海)利用单摆验证小球平抛运动规律,设计方案如图(a)所示,在悬点O正下方有水平放置的炽热的电热丝P,当悬线摆至电热丝处时能轻易被烧断;MN为水平木板,已知悬线长为L,悬点到木板的距离OO′=h(h>L).

(1)电热丝P必须放在悬点正下方的理由是:
(2)将小球向左拉起后自由释放,最后小球落到木板上的C点,O′C=s,则小球做平抛运动的初速度为v0=
(3)在其他条件不变的情况下,若改变释放小球时悬线与竖直方向的夹角θ,小球落点与O′点的水平距离s将随之改变,经多次实验,以s2为纵坐标、cosθ为横坐标,得到如图(b)所示图象.则当θ=30?时,s为

(1)电热丝P必须放在悬点正下方的理由是:
保证小球沿水平方向抛出
保证小球沿水平方向抛出
.(2)将小球向左拉起后自由释放,最后小球落到木板上的C点,O′C=s,则小球做平抛运动的初速度为v0=
s
|
s
.
|
(3)在其他条件不变的情况下,若改变释放小球时悬线与竖直方向的夹角θ,小球落点与O′点的水平距离s将随之改变,经多次实验,以s2为纵坐标、cosθ为横坐标,得到如图(b)所示图象.则当θ=30?时,s为
0.52
0.52
m;若悬线长L=1.0m,悬点到木板间的距离OO′为1.5
1.5
m.分析:(1)只有保证小球沿水平方向抛出才能保证物体做平抛运动.
(2)根据平抛运动的规律可求得物体平抛运动的速度.
(3)小球在抛出后有s=vt,h-L=
gt2而平抛前有mg(L-Lcosθ)=
mv2
故有s2=4(h-L)L(1-cosθ)
将cosθ=0时s2=2,和cos30°=
代入解得s=0.52m.
将l=1.0m代入s2=4(h-L)L(1-cosθ)利用图象可得h=1.5m.
(2)根据平抛运动的规律可求得物体平抛运动的速度.
(3)小球在抛出后有s=vt,h-L=
| 1 |
| 2 |
| 1 |
| 2 |
故有s2=4(h-L)L(1-cosθ)
将cosθ=0时s2=2,和cos30°=
| ||
| 2 |
将l=1.0m代入s2=4(h-L)L(1-cosθ)利用图象可得h=1.5m.
解答:解:(1)由于在烧断细线前小球做圆周运动,故速度方向沿切线方向,所以只有在悬点正下方物体的速度沿水平方向,要小球做平抛运动,则小球平抛的初速度只能沿水平方向,故只有保证小球沿水平方向抛出才能保证物体做平抛运动.(2)由于小球做平抛运动故有在水平方向有s=vt
在竖直方向有h-L=
gt2…①
故有v=s
;
(3)变释放小球时悬线与竖直方向的夹角θ时,小球平抛的速度v,则有mg(L-Lcosθ)=
mv2…②
则物体在水平方向的位移s=vt…③
联立①②③可得
s2=4(h-L)L(1-cosθ)
显然当cosθ=0时,即有2=4(h-L)L(1-cosθ)
当θ=30°时,cosθ=
,s2=4(h-L)L(1-
)
故有
=
=
故s=
=
=0.52m.
s2=4(h-L)L(1-cosθ)
故当l=1.0m时有:2=4(h-1)×1,
即h-1=0.5
h=1.5.
故答案为(1)保证小球沿水平方向抛出.
(2)s
;
(3)0.52,1.5.
在竖直方向有h-L=
| 1 |
| 2 |
故有v=s
|
(3)变释放小球时悬线与竖直方向的夹角θ时,小球平抛的速度v,则有mg(L-Lcosθ)=
| 1 |
| 2 |
则物体在水平方向的位移s=vt…③
联立①②③可得
s2=4(h-L)L(1-cosθ)
显然当cosθ=0时,即有2=4(h-L)L(1-cosθ)
当θ=30°时,cosθ=
| ||
| 2 |
| ||
| 2 |
故有
| 2 |
| s2 |
| 1 | ||||
1-
|
| 2 | ||
2-
|
故s=
2-
|
| 0.268 |
s2=4(h-L)L(1-cosθ)
故当l=1.0m时有:2=4(h-1)×1,
即h-1=0.5
h=1.5.
故答案为(1)保证小球沿水平方向抛出.
(2)s
|
(3)0.52,1.5.
点评:本题难度中等,在解(3)时一定要充分利用s2-cosθ所提供的信息进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2007?上海)一置于铅盒中的放射源发射的α、β和γ射线,由铅盒的小孔射出,在小孔外放一铝箔后,铝箔后的空间有一匀强电场.进入电场后,射线变为a、b两束,射线a沿原来方向行进,射线b发生了偏转,如图所示,则图中的射线a为
(2007?上海)一置于铅盒中的放射源发射的α、β和γ射线,由铅盒的小孔射出,在小孔外放一铝箔后,铝箔后的空间有一匀强电场.进入电场后,射线变为a、b两束,射线a沿原来方向行进,射线b发生了偏转,如图所示,则图中的射线a为 (2007?上海)某同学设计了如图(a)所示电路研究电源输出功率变化情况.电源E电动势、内电阻恒定,R1为滑动变阻器,R2、R3为定值电阻,A、V为理想电表.
(2007?上海)某同学设计了如图(a)所示电路研究电源输出功率变化情况.电源E电动势、内电阻恒定,R1为滑动变阻器,R2、R3为定值电阻,A、V为理想电表.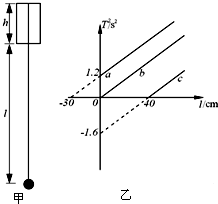 (2007?上海模拟)在“用单摆测定重力加速度”的实验中,将一单摆装置竖直悬于某一深度为h(未知)且开口向下的固定小筒中(单摆的下部分露于筒外),如图甲所示.将悬线拉离平衡位置一个小角度后由静止释放,设单摆摆动过程中悬线不会碰到筒壁.如果本实验的长度测量工具只能测量出筒下端口到摆球球心之间的距离l,并通过改变l 而测出对应的摆动周期T,再以T2为纵轴、l 为横轴,作出T2-l 图象,则可以由此图象得出我们想要测量的物理量.
(2007?上海模拟)在“用单摆测定重力加速度”的实验中,将一单摆装置竖直悬于某一深度为h(未知)且开口向下的固定小筒中(单摆的下部分露于筒外),如图甲所示.将悬线拉离平衡位置一个小角度后由静止释放,设单摆摆动过程中悬线不会碰到筒壁.如果本实验的长度测量工具只能测量出筒下端口到摆球球心之间的距离l,并通过改变l 而测出对应的摆动周期T,再以T2为纵轴、l 为横轴,作出T2-l 图象,则可以由此图象得出我们想要测量的物理量.