题目内容
 (2013?湖北模拟)如图所示xoy平面直角坐标系中,第一象限内有一个圆形有界匀强磁场(图中未画出),x轴下方分布斜向左上与y轴方向夹角θ=45°的匀强电场;在x轴上放置有一挡板,长0.16m,板的中心与O点重合.今有一带正电粒子从y轴上某点P以初速度v0=40m/s与y轴负方向成45°角射入第一象限,经过圆形有界磁场恰好偏转90°,并从A点进入下方电场,如图所示.已知A点坐标(0.4m,0),匀强磁场垂直纸面向外,磁感应强度大小B=
(2013?湖北模拟)如图所示xoy平面直角坐标系中,第一象限内有一个圆形有界匀强磁场(图中未画出),x轴下方分布斜向左上与y轴方向夹角θ=45°的匀强电场;在x轴上放置有一挡板,长0.16m,板的中心与O点重合.今有一带正电粒子从y轴上某点P以初速度v0=40m/s与y轴负方向成45°角射入第一象限,经过圆形有界磁场恰好偏转90°,并从A点进入下方电场,如图所示.已知A点坐标(0.4m,0),匀强磁场垂直纸面向外,磁感应强度大小B=
| ||
| 10 |
| q |
| m |
| 2 |
(1)常电粒子在圆形磁场中运动时,轨迹半径多大?
(2)圆形磁场区域的最小面积为多少?
(3)为使粒子出电场时不打在挡板上,电场强度应满足什么要求?
分析:粒子在磁场中受洛伦兹力作用做圆周远动,洛伦兹力充当向心力,可求轨道半径;
借助几何关系可求磁场最小面积;
粒子进入电场后做类平抛运动,根据平抛运动规律可求电场强度E,根据挡板的长度,可得电场强度的范围
借助几何关系可求磁场最小面积;
粒子进入电场后做类平抛运动,根据平抛运动规律可求电场强度E,根据挡板的长度,可得电场强度的范围
解答:解:(1)设带电粒子在磁场中偏转的轨道半径为R,则
由洛伦兹力提供向心力可得:qvB=
故:R=
=
=0.2m;
(2)由几何关系可得圆形磁场的最小半径为:r=
R
圆形磁场的最小面积:S=πr2=6.28×10-2m2
(3)粒子进入电场后做类平抛运动,射出电场的位置距离A点L,
则:Lcos45°=v0t
Lsin45°=
at2
且:qE=ma
解得:E=
若要使粒子不打在挡板上,则L>0.48m,或L<0.32m
解得:E<6.67N/C或E>10N/C
答:(1)常电粒子在圆形磁场中运动时,轨迹半径为0.2m;
(2)圆形磁场区域的最小面积为6.28×10-2m2;
(3)为使粒子出电场时不打在挡板上,电场强度应满足:E<6.67N/C或E>10N/C.
由洛伦兹力提供向心力可得:qvB=
| mv02 |
| R |
故:R=
| mv0 |
| qB |
| 40 | ||||||
|
(2)由几何关系可得圆形磁场的最小半径为:r=
| ||
| 2 |
圆形磁场的最小面积:S=πr2=6.28×10-2m2
(3)粒子进入电场后做类平抛运动,射出电场的位置距离A点L,
则:Lcos45°=v0t
Lsin45°=
| 1 |
| 2 |
且:qE=ma
解得:E=
2
| ||||
| qL |
若要使粒子不打在挡板上,则L>0.48m,或L<0.32m
解得:E<6.67N/C或E>10N/C
答:(1)常电粒子在圆形磁场中运动时,轨迹半径为0.2m;
(2)圆形磁场区域的最小面积为6.28×10-2m2;
(3)为使粒子出电场时不打在挡板上,电场强度应满足:E<6.67N/C或E>10N/C.
点评:本题是粒子在混合场中运动,根据粒子在场中的运动特点,结合几何关系可列式求解,难度适中.

练习册系列答案
相关题目
 (2013?湖北模拟)在用打点计时器验证机械能守恒定律的实验中,使质量为m=1.00kg的重物自由下落,打点计时器在纸带上打出一系列的点,选取一条符合实验要求的纸带如图所示.O为第一个点,A、B、C为从合适位置开始选取连续点中的三个点.已知打点计时器每隔0.02s打一个点,当地的重力加速度为g=9.80m/s2,那么:
(2013?湖北模拟)在用打点计时器验证机械能守恒定律的实验中,使质量为m=1.00kg的重物自由下落,打点计时器在纸带上打出一系列的点,选取一条符合实验要求的纸带如图所示.O为第一个点,A、B、C为从合适位置开始选取连续点中的三个点.已知打点计时器每隔0.02s打一个点,当地的重力加速度为g=9.80m/s2,那么: (2013?湖北模拟)如图所示,某同学骑电动车以 10m/s的速度匀速驶向路口,当行驶至距路口停车线20m处时,绿灯还有3s熄灭.而该同学在绿灯熄灭时刚好停在停车线处,则该同学运动的v-t图象可能是( )
(2013?湖北模拟)如图所示,某同学骑电动车以 10m/s的速度匀速驶向路口,当行驶至距路口停车线20m处时,绿灯还有3s熄灭.而该同学在绿灯熄灭时刚好停在停车线处,则该同学运动的v-t图象可能是( )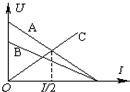 (2013?湖北模拟)如图所示,直线A为电源a的路端电压与电流的关系图象,直线B为电源b的路端电压与电流的关系图象,直线C为一个电阻R的两端电压与电流的关系图象.将这个电阻R分别接到a、b两电源上,那么( )
(2013?湖北模拟)如图所示,直线A为电源a的路端电压与电流的关系图象,直线B为电源b的路端电压与电流的关系图象,直线C为一个电阻R的两端电压与电流的关系图象.将这个电阻R分别接到a、b两电源上,那么( ) (2013?湖北模拟)一定质量的理想气体从状态A变化到状态B,再变化到状态C,其状态变化过程的p-V图象如图所示.已知该气体在状态A时的温度为27℃.则:
(2013?湖北模拟)一定质量的理想气体从状态A变化到状态B,再变化到状态C,其状态变化过程的p-V图象如图所示.已知该气体在状态A时的温度为27℃.则: (2013?湖北模拟)如图所示,实线和虚线分别是沿x轴传播的一列简谐横波在t=0和t=0.06s时刻的波形图.已知在t=0时刻,x=1.5m处的质点向y轴正方向运动.
(2013?湖北模拟)如图所示,实线和虚线分别是沿x轴传播的一列简谐横波在t=0和t=0.06s时刻的波形图.已知在t=0时刻,x=1.5m处的质点向y轴正方向运动.