题目内容
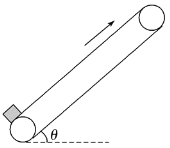
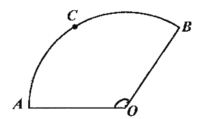
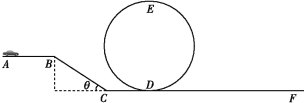
【题目】某次电动小汽车表演如图所示，质量为2 kg的小汽车从平台A处出发，以v0=5m/s经过B处飞越斜坡，恰落在斜坡底端的C点，着地之后瞬间车速变为4 m/s，之后沿平直轨道CD运动，到达D点时关闭发动机，进入半径为1.8 m圆轨道，运动一周后又进入水平轨道向右运动，直到停车点F时刚好停下。已知小汽车与水平面的摩擦阻力恒为重力的0.1倍，AC段运动过程中风力较大，可简化为受0.8N的水平向右的作用力，竖直方向的空气作用力忽略不计，过了C点后无风，不计空气作用力。圆轨道可视为光滑。已知AB段长度x0=3m，AB平台高1.25 m，CD段长度x2=2m，DF段长度x3=50m。小汽车的自身长度可忽略，g取10 m/s2，求：
(1)斜坡倾角的正切值tanθ；
(2)要使小汽车完成上述运动，CD段电动机至少提供多少能量?
(3)若DF阶段启用动力回收系统，回收效率为30%，则此段小汽车能滑行多远?
【答案】(1)
；(2)88J；(3)35m
【解析】
(1)飞跃斜坡过程，竖直的分运动为自由落体运动，水平方向的分运动为匀加速直线运动，水平加速度
风力
得
竖直方向有
水平位移
得
(2)小汽车与水平轨道的摩擦阻力
设小汽车通过D点、E点的速度分别为
和 
，如果小汽车恰能做完整的圆周运动，在E点应满足
从D到E的过程，运用动能定理有
得
根据机械能守恒定律，运动一周回到D点的速度仍为
设之后小汽车匀减速运动发生的位移为L
得
，故小汽车到不了终点线，若要到达终点线，小汽车的速度至少为
得
C点到D点，电动机提供的能量至少为E，有
解得
得
(3)若在DF阶段开启动力回收系统，回收效率30%，即有70%的能量用于克服摩擦力做功
得
练习册系列答案
相关题目
