Question

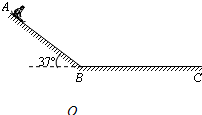（2009?广州三模）（1）在海滨游乐场里有一种滑沙的游乐活动．如图所示，人坐在滑板上从斜坡的高处由静止开始滑下，滑到斜坡底端B点后沿水平的滑道再滑行一段距离到C点停下来．若某人和滑板的总质量m=60.0kg，滑板与斜坡滑道和水平滑道间的动摩擦因数相同，大小为μ=0.50，斜坡的倾角θ=37°．斜坡与水平滑道间是平滑连接的，整个运动过程中空气阻力忽略不计．试求：人从斜坡滑下的加速度为多大？若出于场地的限制，水平滑道的最大距离为L=20.0m，则人在斜坡上滑下的距离AB应不超过多少？（sin37°=0.6，cos37°=0.8）
（2）地球绕太阳的公转可认为是匀速圆周运动．已知地球的半径为R，地球表面的重力加速度为g，地球绕太阳公转的周期为T，太阳发出的光经时间t₀到达地球表面，光在真空中的传播速度为c．太阳到地球表面的距离远远大于地球的半径．根据以上条件推出太阳的质量M与地球的质量m之比．

Answer 1

分析：（1）人与滑板由静止从粗糙斜面滑下后，又滑上粗糙水平面最后停止．在斜面上对其进行受力分析，再进行力的合成求出合力，运用牛顿第二定律可算出加速度．当人与滑板从静止到停止，先做匀加速后做匀减速，由运动学公式与牛顿运动定律可求出滑下的最大距离．
（2）根据太阳发出的光经过时间t到达地球，求出地球与太阳之间的距离，地球绕太阳做匀速圆周运动，根据万有引力周期公式求出太阳的质量，再根据地球表面重力等于万有引力求出地球的质量即可求解．

解答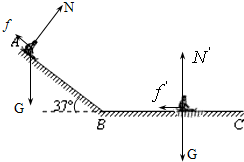：解：（1）人在斜面上受力如图所示，建立图示坐标系，设人在斜坡上滑下的加速度为a₁，
由牛顿第二定律有mgsin37°-f=ma₁   
N=mgcos37°
又因为f=μN          
解得a₁=2m/s²
设滑板在水平滑道上时的加速度为a₂
-μmg=ma₂
解得：a2=-μg=-5m/s2
根据位移速度公式得：vB=

0-2a2L

=

0-2×(-5)×20

m/s=10

2

m/s    
所以SAB=

v 2 B

2a1

=

200

2×2

m=50m
（2）设地球绕太阳做匀速圆周运动的半径为r，角速度为ω．
根据万有引力定律和牛顿第二定律：
G

Mm

r2

=mω2r      
又ω=

2π

T

r=ct₀
在地球表面附近的小物体m₀，其重力等于万有引力，则有：
G

mm0

R2

=m0g
解得：

M

m

=

4π2c3t03

T2R2g

答：（1）人从斜坡滑下的加速度为2m/s²，人在斜坡上滑下的距离AB应不超过50m；
（2）太阳的质量M与地球的质量m之比为

4π2c3t03

T2R2g

．

点评：（1）对研究对象的进行受力分析与运动分析，再由运动学公式与牛顿运动定律相结合．同时第二个小问可以用动能定理来处理．
（2）本题主要考查了万有引力公式的直接应用，知道天体运动中只能求出中心天体的质量，难度适中．