题目内容
【题目】如图所示,真空中有以O1为圆心、r半径的圆形匀强磁场区域,坐标原点O为圆形磁场边界上的一点。磁场的磁感应强度大小为B,方向垂直于纸面向外。x=r的虚线右侧足够大的范围内有方向竖直向下、大小为E的匀强电场。从O点在纸面内向各个方向发射速率相同的质子,速度方向与x轴正方向成120°角的质子,经磁场偏转后又垂直射入电场,到达x轴上的P点(图中未画出)。已知质子的电荷量为e、质量为m,质子重力可忽略。

(1)求质子射入磁场时的速度大小;
(2)求质子从坐标原点O到x轴上的P点所需的时间;
(3)若质子沿y釉正方向射入磁场,在离开磁场前的某一时刻,磁场方向不变、大小突然变为B1,此后质子恰好被束缚在该圆形磁场中,则B1的最小值为多少?
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】
质子射入磁场后做匀速圆周运动,根据洛伦兹力提供向心力,即可求得质子射入磁场时的速度大小;
质子沿y轴正方向射入,在磁场中以O2为圆心转过![]() 圆弧后从A点垂直于电场方向进入电场.在磁场中的运动为
圆弧后从A点垂直于电场方向进入电场.在磁场中的运动为![]() 周期;质子进入电场后做类平抛运动,将运动沿电场方向和垂直于电场的方向分解,即可求得粒子在电场中运动的时间;t=t1+t2。
周期;质子进入电场后做类平抛运动,将运动沿电场方向和垂直于电场的方向分解,即可求得粒子在电场中运动的时间;t=t1+t2。
(1) 设质子射磁场时的速度为v.质子射入磁场后做匀速圆周运动,质子的轨迹如图所示
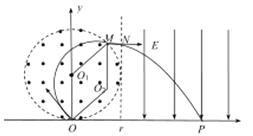
由几何关系知,质子在磁场中的偏转半径为R=r,
由牛顿第二定律:![]()
解得:![]() ;
;
(2)质子在磁场中运动的周期![]()
质子在磁场中的运动轨迹所对应的圆心角为1200
运动时间为![]()
质子离开磁场做匀速直线运动,匀速运动位移为:![]()
匀速运动的时间为:![]()
质子垂直射入电场做类平抛运动,设在电场中的运动时间为![]()
竖直位移为![]()
根据匀变速直线运动的规律![]()
其中![]() 解得:
解得:![]()
质子从O点到达x轴的时间![]() ;
;
(3)若粒子运动轨迹的圆心为O3,如图所示
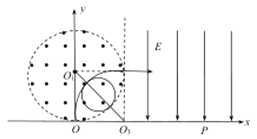
当质子运动到轨迹与O1O3连线交点处时,仅改变磁场大小,粒子运动的半径最大,即B1对应最小,
由几何关系得,最大半径![]()
由![]()
解得:![]() 。
。

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案