题目内容
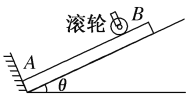
【题目】如图所示,电动机带动滚轮做逆时针匀速转动,在滚轮的摩擦力作用下,将一金属板从光滑斜面底端A送往斜面上端,斜面倾角θ=30°,滚轮与金属板的切点B到斜面底端A距离L=6.5 m,当金属板的下端运动到切点B处时,立即提起滚轮使其与板脱离。已知板的质量m=1×103 kg,滚轮边缘线速度v=4 m/s,滚轮对板的正压力FN=2×104 N,滚轮与金属板间的动摩擦因数为μ=0.35,g取10 m/s2。求:
(1)在滚轮作用下板上升的加速度大小;
(2)金属板的下端经多长时间到达滚轮的切点B处;
(3)金属板沿斜面上升的最大距离。
【答案】(1) 2 m/s2 (2) 2.625 s (3)8.1 m
【解析】
(1)对金属板受力分析,运用正交分解法,根据牛顿第二定律列方程即可求出加速度.(2)假设金属板一直匀加速上升,求出位移可知还要匀速上升,所以金属板从A到B经历加速上升和匀速上升两个过程,分别求出两个过程的时间.(3)金属从B点向上做匀减速运动,先根据牛顿第二定律求出匀减速的加速度,求出位移,再加上L即为金属板沿斜面上升的最大距离.
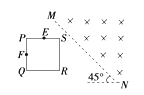
(1) 对金属板受力分析如图所示:
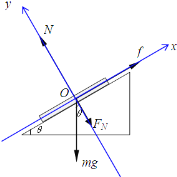
受力正交分解后,沿斜面方向由牛顿第二定律得μFN-mgsinθ=ma1
解得a1=2m/s2
(2)由运动规律得v=a1t1
解得t1=2s
匀加速上升的位移为![]()
匀速上升需时间![]()
共经历t=t1+t2=2.625s
(3)滚轮与金属板脱离后向上做减速运动,由牛顿第二定律得mgsin θ=ma2
解得a2=5m/s2
金属板做匀减速运动,则板与滚轮脱离后上升的距离![]()
金属板沿斜面上升的最大距离为xm=L+x2=6.5m+1.6m=8.1m

练习册系列答案
相关题目