题目内容
9.某实验小组在进行“用单摆测定重力加速度”的实验中,已知单摆在摆动过程中的摆角小于5°;在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t;在测量单摆的摆长时,先用毫米刻度尺测得悬挂后的摆线长(从悬点到摆球的最上端)为L,再用游标卡尺测得摆球的直径为d(读数如图1所示).
(1)该单摆在摆动过程中的周期为$\frac{2t}{n-1}$.
(2)用上述物理量的符号写出求重力加速度的一般表达式g=$\frac{4{π}^{2}(n-1)^{2}(L+\frac{d}{2})}{4{t}^{2}}$.
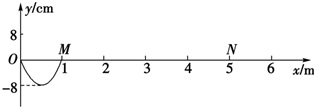
(3)从图可知,摆球的直径为9.30mm.
(4)实验结束后,发现测得的重力加速度的值总是偏大,其原因可能是下述原因中的BD.
A.单摆的悬点未固定紧,振动中出现松动,使摆线增长了
B.把n次摆动的时间误记为(n+1)次摆动的时间
C.以摆线长作为摆长来计算
D.以摆线长与摆球的直径之和作为摆长来计算
(5)实验时,若摆球在垂直纸面的平面内摆动,为了将人工记录振动次数改为自动记录振动次数,在摆球运动最低点的左、右两侧分别放置一激光光源与光敏电阻,如图2所示.光敏电阻与某一自动记录仪相连,该仪器显示的光敏电阻阻值R随时间t的变化图线如图3所示,则该单摆的振动周期为2t0; 若保持悬点到小球顶点的绳长不变,改用直径是原小球直径2倍的另一小球进行实验,则该单摆的周期将变大;图乙中的△t将变大( 填“变大”、“不变”或“变小”).
分析 (1)根据从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t,确定单摆全振动的次数,再求解周期.
(2)单摆的长度为l=L+$\frac{d}{2}$.将摆长、周期代入单摆的周期公式求出重力加速度的表达式g.
(3)游标卡尺主尺与游标尺示数之和是游标卡尺的示数;
(4)对于测量误差可根据实验原理进行分析;
(5)根据实验要求:小球的偏角α在很小(α<5°)时,小球的振动才近似看成简谐运动.在摆球经过最低点时开始计时,产生的时间误差较小.把秒表记录摆球一次全振动的时间作为周期,误差较大,应采用累积法测量周期.在一个周期内两次经过平衡位置,根据该特点结合图象得出单摆的周期.根据单摆的周期公式判断周期的变化.
解答 解:(1)由题,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t,则单摆全振动的次数为N=$\frac{n-1}{2}$,周期T=$\frac{t}{N}$=$\frac{2t}{n-1}$;
(2)单摆的长度为l=L+$\frac{d}{2}$.
由单摆的周期公式T=2π$\sqrt{\frac{l}{g}}$得:g=$\frac{4{π}^{2}(n-1)^{2}(L+\frac{d}{2})}{4{t}^{2}}$;
(3)由图示可知,游标卡尺主尺示数为9.0mm,游标尺示数为6×0.05mm=0.30mm,
游标卡尺所示为:9.0mm+0.30mm=9.30mm;
(4)A、单摆的悬点未固定紧,振动中出现松动,使摆线增长了,所测周期T偏大,由g=$\frac{4{π}^{2}L}{{T}^{2}}$ 可知,所测g偏小,故A错误;
B、把n次摆动的时间误记为(n+1)次摆动的时间,使所测周期变小,计算出的g偏大,故B正确;
C、以摆线长作为摆长来计算,摆长偏小,使所测g偏小,故C错误;
D、以摆线长与摆球的直径之和作为摆长来计算,摆长偏大,求出的g偏大,故D正确;
(5)单摆在一个周期内两次经过平衡位置,每次经过平衡位置,单摆会挡住细激光束,
从R-t图线可知周期为2t0.
摆长等于摆线的长度加上小球的半径,改用直径是原小球直径2倍的另一小球进行实验,
根据单摆的周期公式T=2π$\sqrt{\frac{L}{g}}$,摆长变大,所以周期变大.
再根据$△t=\frac{d}{v}$,可知,图乙中的△t将变大,
故答案为:(1)$\frac{2t}{n-1}$;(2)$\frac{4{π}^{2}(n-1)^{2}(L+\frac{d}{2})}{4{t}^{2}}$;(3)9.30;(4)BD;(5)2t0,变大,变大.
点评 常用仪器的读数要掌握,这是物理实验的基础.掌握单摆的周期公式,从而求解加速度,摆长、周期等物理量之间的关系.单摆的周期采用累积法测量可减小误差.对于测量误差可根据实验原理进行分析.
本题主要考查了在探究影响单摆周期的因素的实验的操作要求,知道单摆的摆长等于摆线的长度加上摆球的半径.

 若取无穷远处为零电势,某一直线上各点的电势φ分布规律可用图中曲线表示,r表示该直线上某点到原点O的距离,r1、r2分别是该直线上A、B两点离原点O的距离.下列说法中正确的是( )
若取无穷远处为零电势,某一直线上各点的电势φ分布规律可用图中曲线表示,r表示该直线上某点到原点O的距离,r1、r2分别是该直线上A、B两点离原点O的距离.下列说法中正确的是( )| A. | O-r0这个区域的电场强度最大 | |
| B. | A点的电场强度可能等于B点的电场强度 | |
| C. | 若r2-r1=r1-r0,则φA-φB=φ0-φA | |
| D. | 将α粒子从A点移到B点,电场力做正功 |
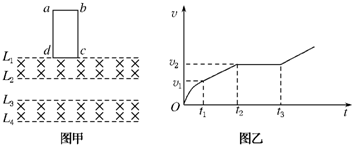
| A. | 在0~t1时间内,通过线圈的电荷量为0.5C | |
| B. | 线圈匀速运动的速度大小为8m/s | |
| C. | 线圈的长度为1m | |
| D. | 0~t3时间内,线圈产生的热量为1.8J |

| A. | Q2带正电 | |
| B. | a、b两点的电势φa>φb | |
| C. | a、b两点电场强度Ea>Eb | |
| D. | 试探电荷从b到a的过程中电势能减小 |
| A. | 空气相对湿度越大时,水蒸发越快 | |
| B. | 物体的温度越高,分子平均动能越大 | |
| C. | 第二类永动机不可能制成是因为它违反了热力学第一定律 | |
| D. | 对一定质量的气体在等容加热,气体压强将增大 |
| A. | 一定温度下,水的饱和汽的压强是一定的 | |
| B. | 改进内燃机结构,提高内燃机内能转化率,最终可能实现内能完全转化为机械能 | |
| C. | 大颗粒的盐磨成了细盐,就变成了非晶体 | |
| D. | 气体温度每升高1K所吸收的热量与气体经历的过程有关 | |
| E. | 大量气体分子做无规则运动,速率有大有小,但分子的速率是按照一定规律分布的 |
 如图是某同学用来探究“小车的加速度与外力关系”的实验装置示意图,轨道上的B点固定一光电门,将连接小车的细线跨过滑轮系住钩码,在A点释放小车,测出小车上挡光片通过光电门的时间为△t.
如图是某同学用来探究“小车的加速度与外力关系”的实验装置示意图,轨道上的B点固定一光电门,将连接小车的细线跨过滑轮系住钩码,在A点释放小车,测出小车上挡光片通过光电门的时间为△t.