题目内容
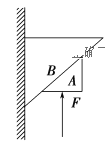
【题目】如图所示,用两根完全相同的橡皮筋M、N将两个质量均为m=1 kg的可视为质点的小球A、B拴接在一起,并悬挂在水平天花板上,在小球A上施加一水平向左的恒力F,当系统处于静止状态时,橡皮筋M与竖直方向的夹角为60°。假设两橡皮筋的劲度系数均为k=5 N/cm,且始终处在弹性限度以内,重力加速度取g=10 m/s2。则( )
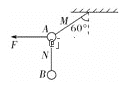
A. 橡皮筋M的伸长量为4 cm B. 橡皮筋N的伸长量为2 cm
C. 水平恒力的大小为![]() D. 水平恒力的大小为
D. 水平恒力的大小为![]()
【答案】BD
【解析】
先对B球受力分析,求出N对B的拉力,根据胡克定律求出N的伸长量,再对A球受力分析,根据平衡条件求出M的拉力以及F,再根据胡克定律求出M的伸长量。
小球B处于静止状态,则N对B的拉力F1=mg=10N,根据胡克定律得:橡皮筋N的伸长量为:![]() ,对A球受力分析,受到重力、N的拉力F1,M的拉力F2以及F作用,处于平衡状态,根据平衡条件得:
,对A球受力分析,受到重力、N的拉力F1,M的拉力F2以及F作用,处于平衡状态,根据平衡条件得:![]() ;
;![]() ,解得:F=20
,解得:F=20![]() N,F2=40N,根据胡克定律得:橡皮筋M的伸长量为:
N,F2=40N,根据胡克定律得:橡皮筋M的伸长量为:![]() ,故AC错误,BD正确;故选BD。
,故AC错误,BD正确;故选BD。

练习册系列答案
相关题目