题目内容
如图所示,某货场需将质量为m1=100kg的货物(可视为质点)从高处运送至地面,为避免货物与地面发生撞击,现利用固定于地面的光滑四分之一圆轨道,使货物由轨道顶端无初速滑下,轨道半径R=1.8m,地面上紧靠轨道放置一木板A,长度为l=2m,质量为m2=100kg,木板上表面与轨道末端相切.货物与木板间的动摩擦因数为μ1,木板与地面间的动摩擦因数μ2=0.2(最大静摩擦力等于滑动摩擦力,取g=10m/s2)
(1)求货物到达圆轨道末端时对轨道的压力.
(2)若货物滑上木板A时,要使木板A不动,求μ1应满足的条件.

(1)求货物到达圆轨道末端时对轨道的压力.
(2)若货物滑上木板A时,要使木板A不动,求μ1应满足的条件.

(1)货物下滑时,由动能定理得:m1gR=
m1v2-0,
在轨道末端,由牛顿第二定律得:F-mg=m
,
解得F=3000N,
由牛顿第三定律得,货物对轨道的压力F′=F=3000N;
(2)木板刚好不动时,μ1m1g=μ2(m1+m2)g,
解得μ1=0.4,当μ1≤0.4时木板A不动;
答:(1)货物到达圆轨道末端时对轨道的压力为3000N.
(2)若货物滑上木板A时,要使木板A不动,μ1应满足的条件是μ1≤0.4.
| 1 |
| 2 |
在轨道末端,由牛顿第二定律得:F-mg=m
| v2 |
| R |
解得F=3000N,
由牛顿第三定律得,货物对轨道的压力F′=F=3000N;
(2)木板刚好不动时,μ1m1g=μ2(m1+m2)g,
解得μ1=0.4,当μ1≤0.4时木板A不动;
答:(1)货物到达圆轨道末端时对轨道的压力为3000N.
(2)若货物滑上木板A时,要使木板A不动,μ1应满足的条件是μ1≤0.4.

练习册系列答案
相关题目
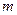 、
、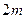 的小球
的小球 、
、 分别固定在长为
分别固定在长为 的轻杆两端,轻杆可绕过中点的水平轴在竖直平面内无摩擦转动,当杆处于水平时静止释放,直至杆转到竖直位置的过程中,杆对小球
的轻杆两端,轻杆可绕过中点的水平轴在竖直平面内无摩擦转动,当杆处于水平时静止释放,直至杆转到竖直位置的过程中,杆对小球