题目内容
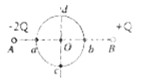
【题目】如图所示，真空中竖直平面内的xOy坐标系的第Ⅱ象限中，有一个紧靠y轴且下极板与x轴重合的平行板电容器，两极板间距离d=0.3m，电容器上极板带正电、下极板带负电；在y轴的右侧有一以（0.2m，0）为圆心的圆形匀强磁场区域，该区域的半径R=0.2m，磁场的磁感应强度大小B=1T、方向垂直于纸面向里；在y=R的虚线上方足够大的范围内，有电场强度大小E=6×106N/C、方向水平向左的匀强电场.一带正电粒子（重力不计）从电容器左侧两极板正中间平行x轴方向射入，结果恰好从坐标原点O沿与x轴正方向斜向下成30°角方向射入磁场，经过一段时间后由P点穿出磁场，最后由M点（P点和M点没有在图中标出）穿过y轴.已知粒子在磁场中做匀速圆周运动的半径也为R，粒子的比荷
.求：
（1）电容器的极板长度L；
（2）P点和M点的坐标；
（3）粒子由O点运动到M点所用的时间t.
【答案】(1) 
(2) 
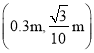,（0，0.4m） (3) 
【解析】
粒子的运动轨迹分为在平行板电容器中的偏转、在磁场中的匀速圆周运动、在磁场和电场之间的匀速直线运动以及在电场中的类平抛运动四个阶段，如图所示.
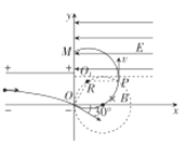
（1）设粒子射入电容器的速度大小为
，在电容器中运动的加速度大小为a、时间为
，到达坐标原点O时沿竖直方向的分速度大小为vy，有：
由几何关系有：
解得：
.
（2）设粒子在磁场中做圆周运动的速度大小为v，有：
解得：
由几何关系知，粒子在磁场中转过120°后，沿y轴正方向先从P点离开磁场，竖直向上匀速运动一段距离后，沿垂直电场方向进入电场.
由几何关系可知，P点到y轴和x轴的距离分别为：
故P点的坐标为
设粒子在电场中做类平抛运动的时间为
，有：
qE=ma'
解得：
M点的纵坐标为：
故M点的坐标为（0，0.4m）.
（3）粒子在磁场中做圆周运动的时间为：
粒子在磁场和电场之间做匀速直线运动的时间为：
故粒子由O点运动到M点所用时间为：
.
