题目内容
如图甲所示,相隔一定距离的竖直边界两侧为相同的匀强磁场区,磁场方向垂直纸面向里,在边界上固定两长为L的平行金属极板MN和PQ,两极板中心各有一小孔S1、S2,两极板间电压的变化规律如图乙所示,正反向电压的大小均为U0,周期为T0.在t=0时刻将一个质量为m、电荷量为-q(q>0)的粒子由S1静止释放,粒子在电场力的作用下向右运动,在t=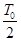 时刻通过S2垂直于边界进入右侧磁场区.(不计粒子重力,不考虑极板外的电场)
时刻通过S2垂直于边界进入右侧磁场区.(不计粒子重力,不考虑极板外的电场)
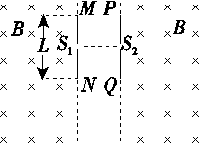
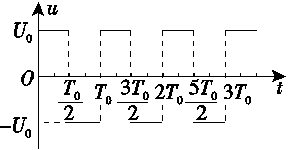
(1)求粒子到达S2时的速度大小v和极板间距d.
(2)为使粒子不与极板相撞,求磁感应强度的大小应满足的条件.
(3)若已保证了粒子未与极板相撞,为使粒子在t=3T0时刻再次到达S2,且速度恰好为零,求该过程中粒子在磁场内运动的时间和磁感应强度的大小.
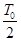 时刻通过S2垂直于边界进入右侧磁场区.(不计粒子重力,不考虑极板外的电场)
时刻通过S2垂直于边界进入右侧磁场区.(不计粒子重力,不考虑极板外的电场)

(1)求粒子到达S2时的速度大小v和极板间距d.
(2)为使粒子不与极板相撞,求磁感应强度的大小应满足的条件.
(3)若已保证了粒子未与极板相撞,为使粒子在t=3T0时刻再次到达S2,且速度恰好为零,求该过程中粒子在磁场内运动的时间和磁感应强度的大小.
(1)d=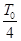
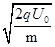 (2)B<
(2)B<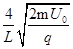 (3)B=
(3)B=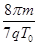
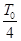
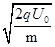 (2)B<
(2)B<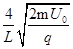 (3)B=
(3)B=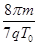
试题分析:(1)粒子由S1至S2的过程,根据动能定理得qU0=
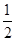 mv2①· (1分)
mv2①· (1分)由①式得v=
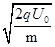 ② (1分)
② (1分)由牛顿第二定律得q
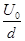 =ma③ (1分)
=ma③ (1分)由运动学公式得d=
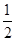 a
a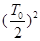 ④ (1分)
④ (1分)联立③④式得d=
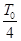
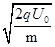 ⑤ (1分)
⑤ (1分)(2)粒子在磁场中做匀速圆周运动的半径为R: qvB=m
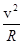 ⑥ (1分)
⑥ (1分)要使粒子在磁场中运动时不与极板相撞,须满足2R>
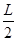 ⑦ (1分)
⑦ (1分)联立②⑥⑦式得B<
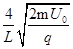 ⑧ (1分)
⑧ (1分)(3)设粒子在两边界之间无场区向左匀速运动时间为t1: d=vt1得t1=
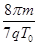 ⑩ (1分)
⑩ (1分)若粒子再次到达S2时速度恰好为零,粒子回到极板间应做匀减速运动,设匀减速运动的时间为t2,根据运动学公式得d=
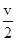 t2?得t2=
t2?得t2=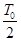 ? (1分)
? (1分)设粒子在磁场中运动的时间为:t=3T0-
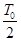 -t1-t2?得t=
-t1-t2?得t=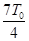 ? (1分)
? (1分)设粒子在匀强磁场中做匀速圆周运动的周期为T=
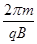 ?· (1分)
?· (1分)可知T=t? (1分)
联立???式得B=
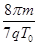 ?· (1分)
?· (1分)点评:本题考查了带电粒子在组合场中的运动,过程复杂,是一道难题,分析清楚粒子的运动过程,作出粒子的运动轨迹,是正确解题的关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目



 时刻才开始从a板运动,那么经过同样长的时间,它将运动到离a板多远的地方?
时刻才开始从a板运动,那么经过同样长的时间,它将运动到离a板多远的地方? t,当t=0时,板间有一个电子正好处于静止状态,下面关于电子以后运动情况的判断哪些是正确的( ).
t,当t=0时,板间有一个电子正好处于静止状态,下面关于电子以后运动情况的判断哪些是正确的( ). 时,电子将有最大速度
时,电子将有最大速度

 中,在
中,在 ,
, 的区域有一对平行金属板M和N,其中N板位于
的区域有一对平行金属板M和N,其中N板位于 轴上,M、N板加有如图所示电压,平行金属板右侧存在沿y轴负向与平行金属板等宽度的匀强电场,场强大小为E,在
轴上,M、N板加有如图所示电压,平行金属板右侧存在沿y轴负向与平行金属板等宽度的匀强电场,场强大小为E,在
 、
、 轴重合。
轴重合。 时刻一质量为
时刻一质量为 ,电量为
,电量为 的带电微粒沿着平金属板的轴线
的带电微粒沿着平金属板的轴线 以初速度
以初速度 向右开始运动,恰从M板右边缘的P点沿
向右开始运动,恰从M板右边缘的P点沿 的速度经Q点进入磁场,Q点为
的速度经Q点进入磁场,Q点为 沿
沿 及右侧电场的宽度
及右侧电场的宽度 ;
; 满足的条件;
满足的条件;

