题目内容
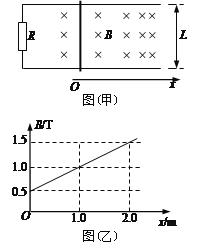
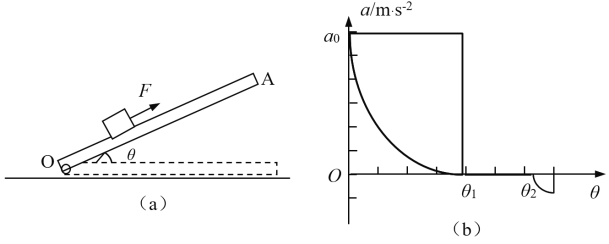
【题目】如图(a),木板OA可绕轴O在竖直平面内转动,木板上有一质量为m=1kg的物块,始终受到平行于斜面、大小为8N的力F的作用。改变木板倾角,在不同倾角时,物块会产生不同的加速度a,如图(b)所示为加速度a与斜面倾角的关系图线。已知物块与木板间的动摩擦因数为μ=0.2,假定物块与木板间的最大静摩擦力始终等于滑动摩擦力。求:(g取10m/s2,sin37=0.6,cos37=0.8)
(1)图线与纵坐标交点a0的大小;
(2)图线与θ轴重合区间为[θ1,θ2],木板处于该两个角度时的摩擦力指向何方?在斜面倾角处于θ1和θ2之间时,物块的运动状态如何?
(3)如果木板长L=2m,倾角为37,物块在F的作用下由O点开始运动,为保证物块不冲出木板顶端,力F最多作用多长时间?
【答案】(1)6m/s2 (2)θ1时,沿斜面向下,θ2时,沿斜面向上;静止 (3)3.1s
【解析】
(1)当木板水平放置时,物块的加速度为a0
此时滑动摩擦力
f = μN = μmg=0.2×1×10 N=2N
由牛顿第二定律
![]()
求得
![]() m/s2=6m/s2;
m/s2=6m/s2;
(2)当木板倾角为θ1时,摩擦力沿斜面向下;当木板倾角为θ2时,摩擦力沿斜面向上;当θ角处于θ1和θ2之间时物块静止;
(3)力F作用时间最长时,撤去力后物块滑到斜面顶端时速度恰好减小到零。
设力F作用时物块的加速度为a1,由牛顿第二定律得:
![]()
撤去力F后物块的加速度大小为a2,由牛顿第二定律:
![]()
设物块不冲出木板顶端,力F最长作用时间为t
则撤去力F时的速度
v=a1t
由题意有:
![]()
由以上各式得:
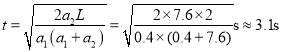

练习册系列答案
相关题目